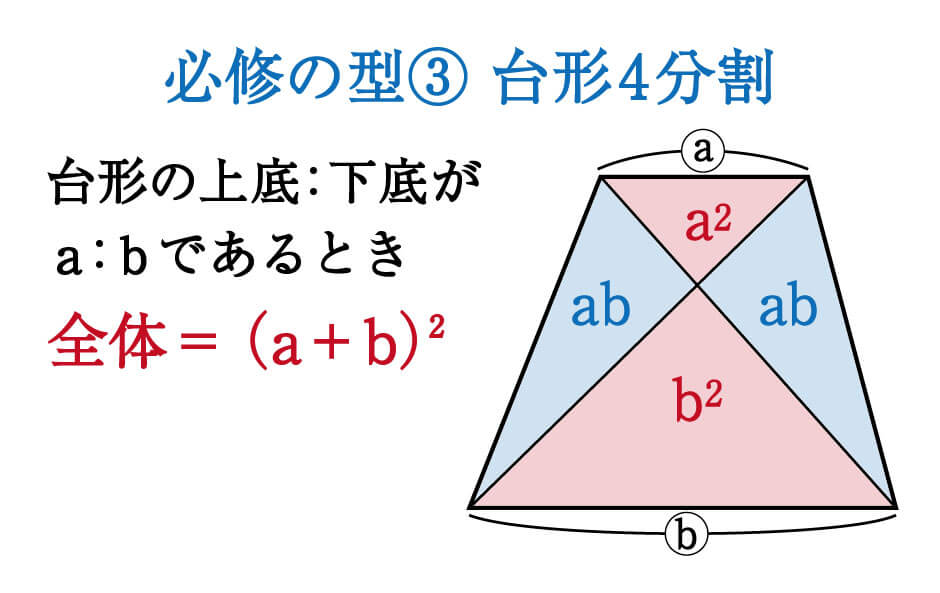
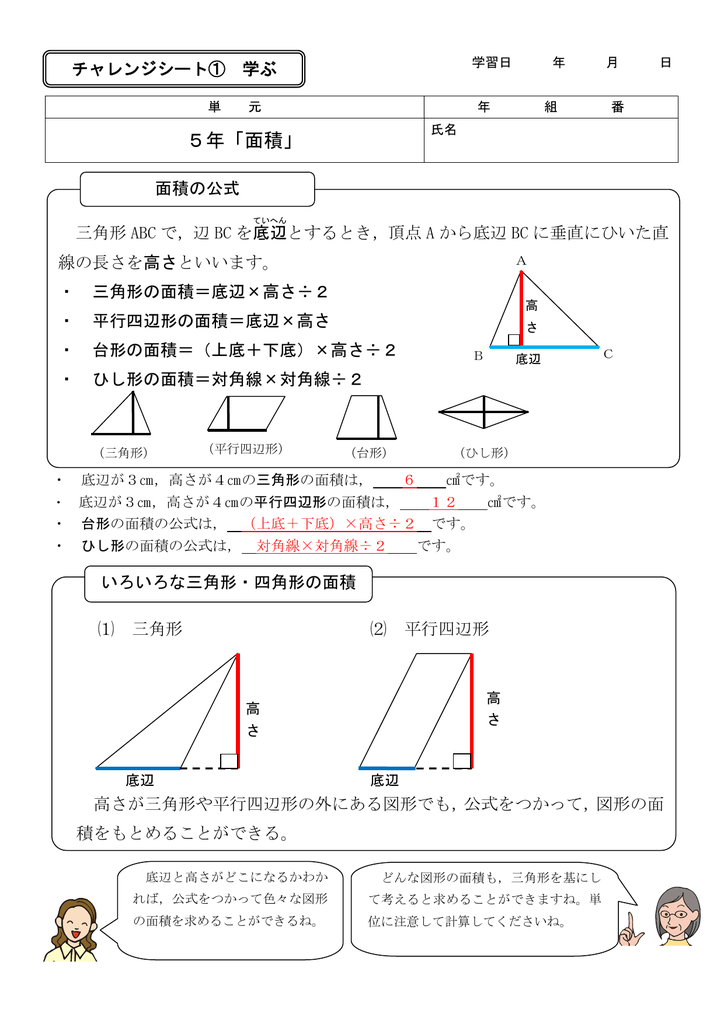
台形に対角線を引いてできる4つの三角形の面積の比は、上底と下底の長さの比を使って 簡単 かんたん に求めることができます。 よく使うので、覚えておくと便利です。・ ひし形の面積の求め方を考え,その方法を 説明する。 ・ ひし形の求積公式を考え,それを適用す る。 ひし形の面積=対角線×対角線÷2 6 底辺の長さを一定にして高さを変えたとき の平行四辺形の面積の変わり方を調べる。 〇 底辺と高さが等しい調和平均は、対角線 ac とbd の交点をp とすると、∆ ∆abp cdp∽ で あることから、2つの三角形の相似比 a b の比に分ける。 このとき、各平均を表す線分により分けられる 2つの台形の面積 s1 と s2 の比を求めてみよう。
等積変形 三角形の面積問題と作図のやり方は 証明問題も紹介 数スタ
台形 対角線 面積 等しい
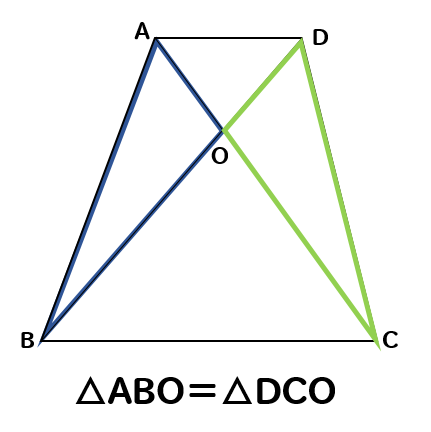
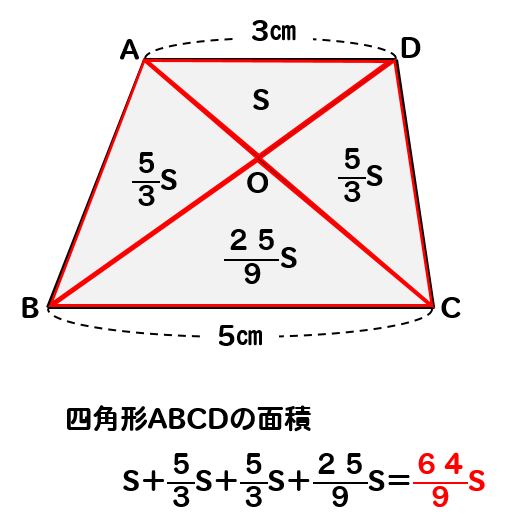
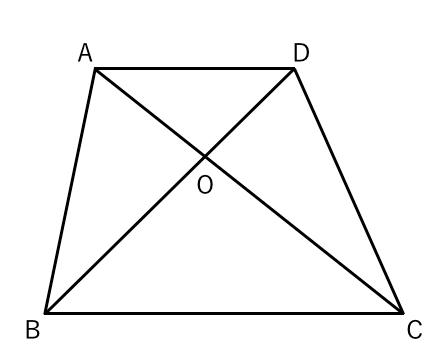
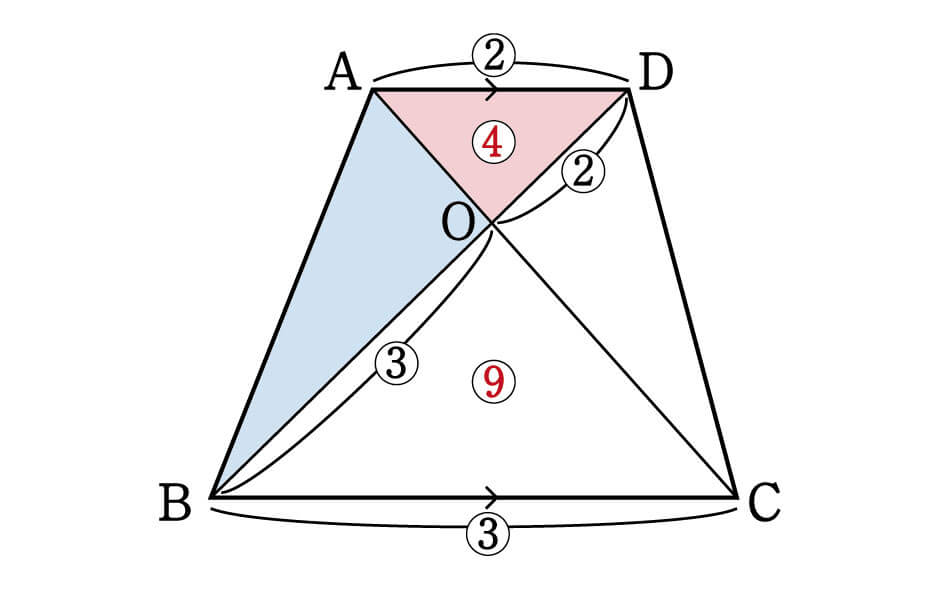
台形 対角線 面積 等しい-ひし形の面積が『対角線×対角線÷2』となる理由 考え方としては\(2\)つあります。 理由1対角線を底辺とした平行四辺形に変形できる ひし形を変形することで、一方の対角線を底辺とする平行四辺形にすることができます。 台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。



5年算数面積2 教え方のポイント
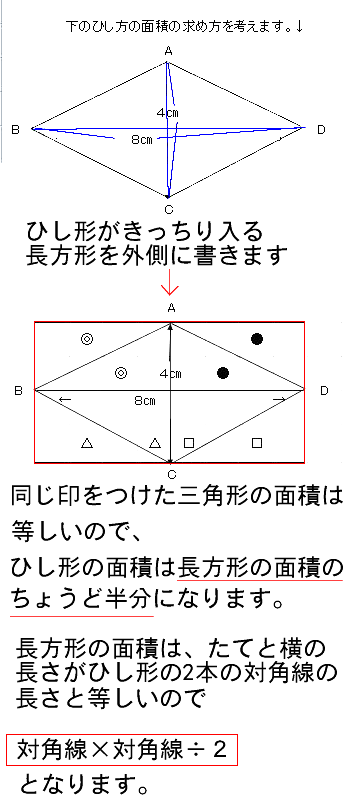
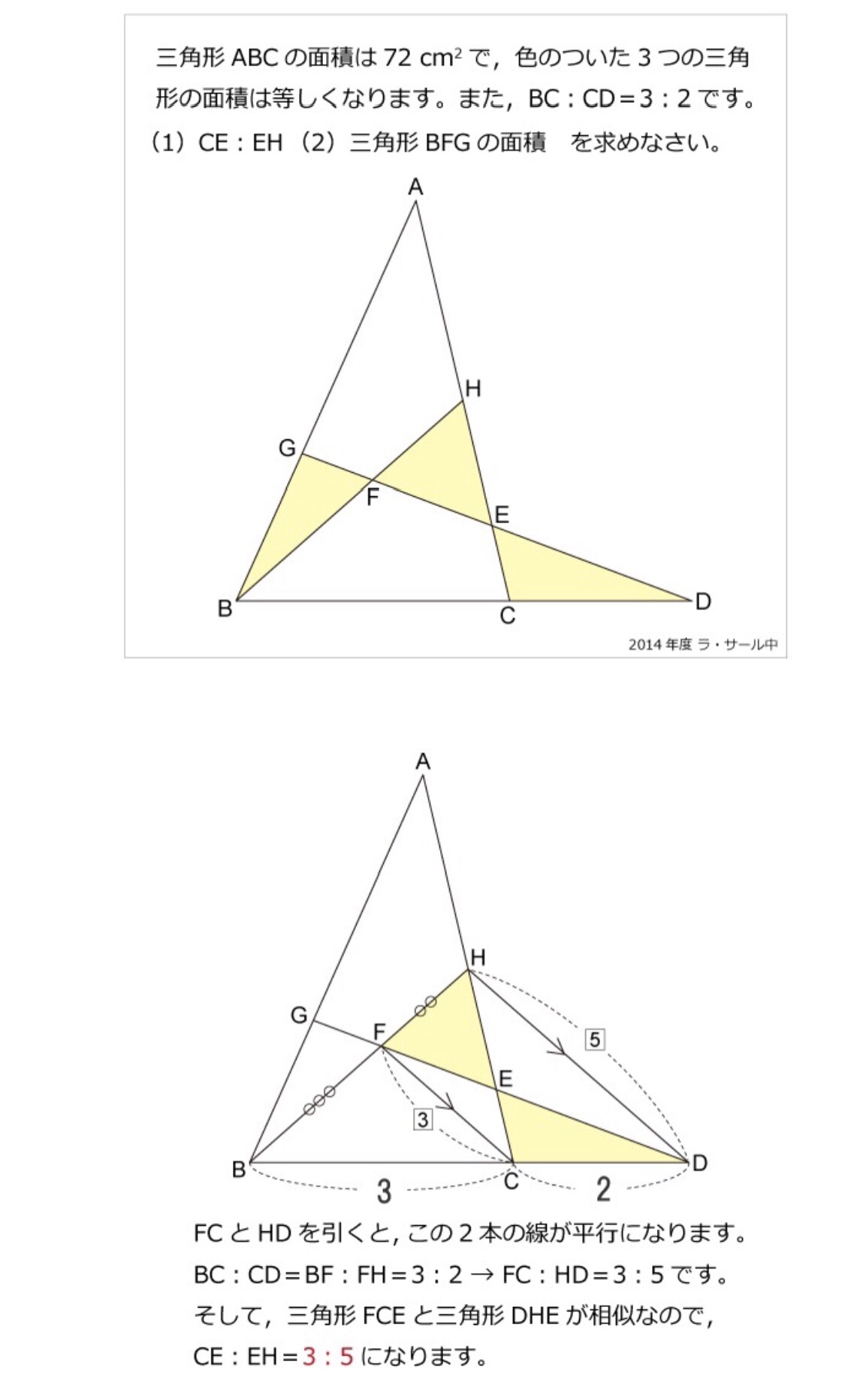
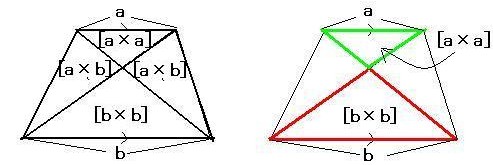
となるため、ひし形の面積は 対角線×対角線÷2 になるというわけです。 対角線を求める計算 ひし形の面積と1つの対角線から、もう1つの対角線の長さを求める場合は、面積に2を掛けて対角線で割れば、もう1つの対角線の長さを求めることができます。長方形の対角線の交点をこのように動かしてみると、先ほど長方形で言えたことはどうですか? S 4つの三角形の面積は等しくなくなる。 S 点Eで十字線を書くと、上の二つの左右の三角形と真中の三角形の面積台形abedの面積は(12+6)×27÷2=243cm 2 。 三角形dfeと三角形abfは相似なので、 三角形dfeと三角形afdと三角形fbeと 三角形abfの面積の比は1:2:2:4。 台形abedの面積を9とすると、黄緑の部分の面積は4。
・ひし形の面積=対角線×対角線÷2 ページの先頭へ 正方形の面積をひし形で考えてみよう 先ほど、「ひし形は正方形のお母さん筋に当たる図形」だと書きましたが、これは、正方形もひし形として面積を求めることが出来ることを意味します。対角線ac=対角線db を証明 問題10 平行な2直線と1つの円が4点で 交わるとき、この4点を結ぶ 四角形は等脚台形であること を証明しなさい。 問題11 四角形abcdにおいて ab=cd、∠b=∠c ならば この四角形abcdは等脚台形で長さが等しければ、面積は等しくなるからね! ポイントは 平行線に挟まれている三角形は高さが等しい! というところです。 それでは、この性質を利用していろんな問題を解説していきますね。 台形の中から等しい三角形を見つける問題
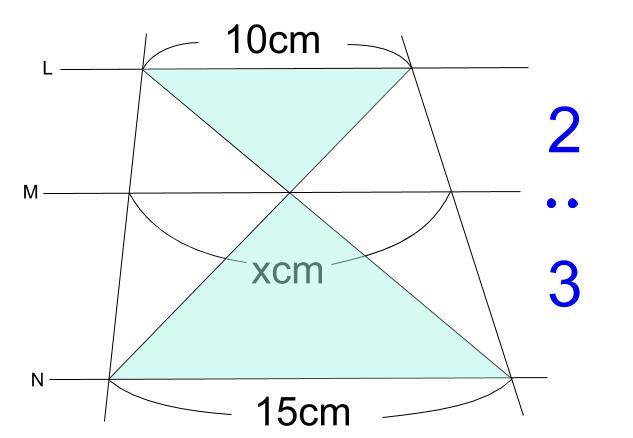
思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 台形を対角線で区切って4つの部分に分けました。アはイよりも9 cm2,ウはエよりも12 cm2小さいとき,アとエの面積比は何対何(台形の面積)=(道の中央線の長さ)×(道幅) このことは、次の図を見れば明らかだろう。 さて、上記のように、中央線の長さから台形の面積を求められる訳だが、この中央線は 当然ながら台形の面積を等分に分けてはいない。(解答) 面積を変えないで図形を変形することを等積変換と言います。 発展問題 等積変換をして、いろいろな図形を作ってみよう。 下の図では、等積変換できるように、頂点は、対角線に対して平行に
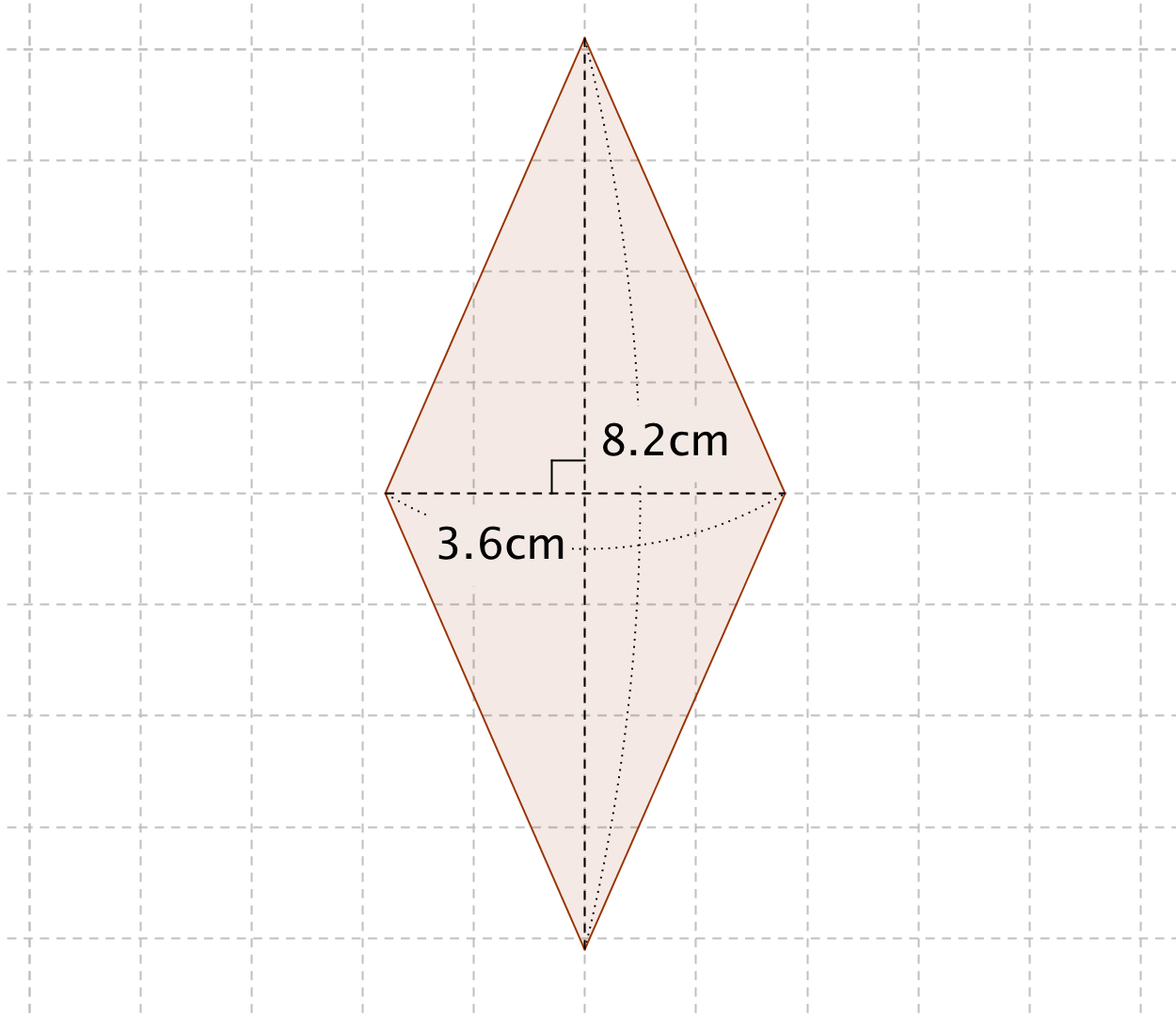



ひし形の面積の公式 算数の公式




等積変形 三角形の面積問題と作図のやり方は 証明問題も紹介 数スタ
台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題※台形の面積は特に忘れやすいので注意が必要です。 正方形はひし形でもあるので 正方形の面積=対角線×対角線÷2 でも求められることも覚えておくといいでしょう。 まだ先ですが円の面積の問題などでもこの知識が役立ちます。



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



長方形への等積変形 面積 量計算 数学教育
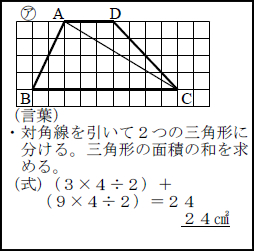
対角線×対角線÷2 という式で求められることに気づかせます。 考え方2 ひし形の面積を求める方法は次のような方法もあります。 どちらの方法でもひし形の面積は 「対角線×対角線÷2」となりますね。こたえあわせ:「対角線×対角線×05」の式によって求まるのは、どんな図形の面積? 円 平方四辺形 台形 菱形 菱形3 必要な長さを測り、面積を求める。 〇 対角線が垂直に交わることを基にして、求積すること ができること 1 台形の面積の求め方をつくる。本時案 〇 図と求積公式をつなぐことを通して、「(上底+下底) ×高さ÷2」という求積公式を捉えること
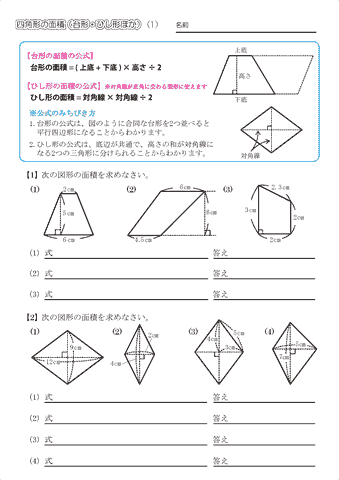



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
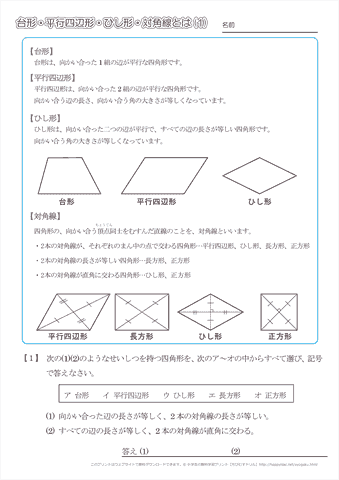
ひし形の面積はそれぞれの対角線をかけて2で割ったものです。 なぜこれでひし形の面積が求められるのかはこちらに解説しています。 ひし形の面積の公式|小学生に教えるための分かりやすい解説 ひし形は平行四辺形の一種です。 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長さが等しい。 イ 2本の対角線が交わった点で, それぞれの対角線が2等分される。 ウ 2本の対角線が垂直に交わって いる。 ひし形の2本の対角線は, に交わっています。
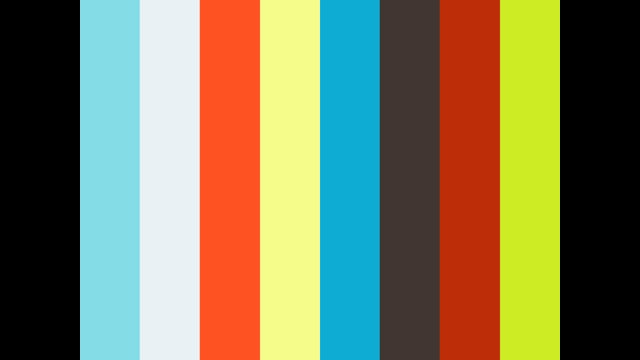



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ



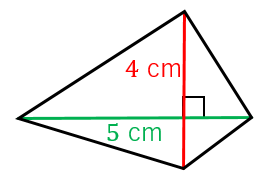
中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
「中点連結定理」は台形(2辺が平行)のような図形にも応用がききますね! 《 例 》 台形abcdにおいて、中点を結んだmnはどのような性質があるでしょうか ad//bc、 am:mb = dn:nc = 1:1 より ad//bc//mn 対角線acを引くと am:mb = dn:nc = ap:pc = 1:1 中点連結定理より「面積= (対角線 1 × 対角線 2)/2」すなわち「A = (d 1 × d 2)/2」 例: 対角線の長さが19mと5mのたこ形があるとします。これの面積は、(19 × 5)/2 = 95/2 = 475 ㎡です。 対角線の長さが分からず、測ることもできない場合、三角関数を用いて求めることができます。区切り面積⑻ 台形 レベル1 対角線で分割 1 例にならって、各部分の面積比をかきこみなさい。※図形は全て台形です。 上の2つの三角形は 高さが等しいから、 面積の比は、底辺の比 で決まります。 例



第5学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館



数学 対角線の入った台形 一角共有の三角形 面積比 集中特訓 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
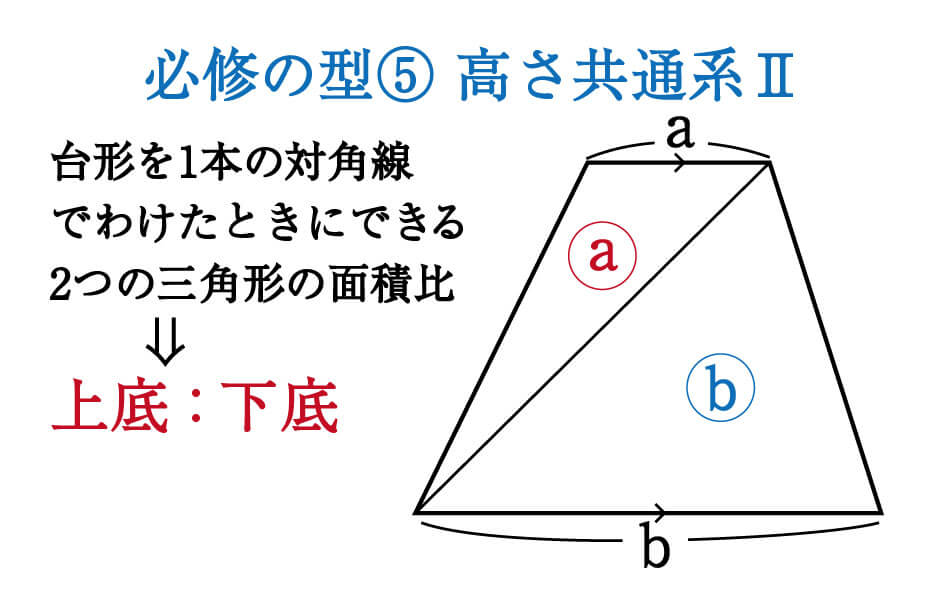
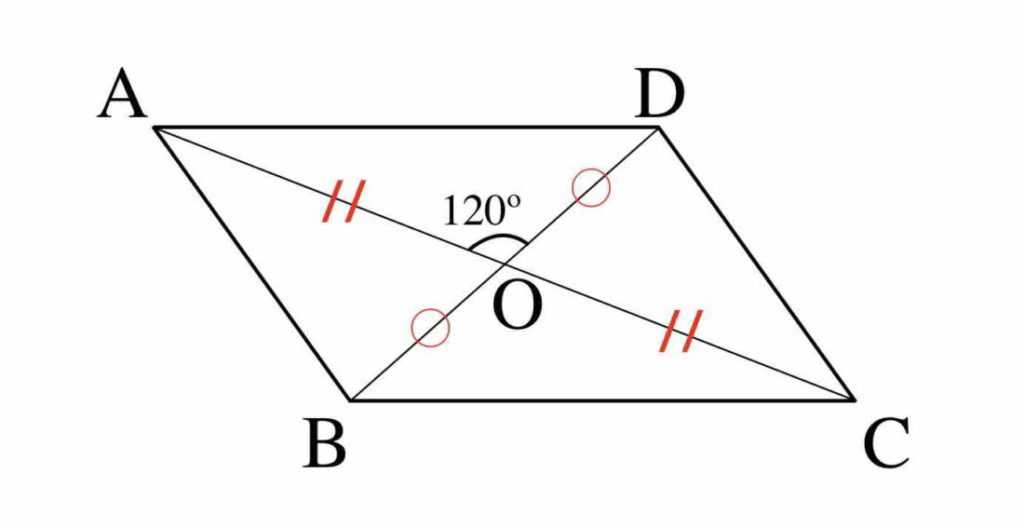
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し 『対角線が直交する特別な台形に限って 対角線×対角線×1/2 という公式ってありましたでしょうか?』 『対角線が直交する特別な台形』に限らず、 『対角線が直交する特別な四角形』なら 対角線×対角線×1/2 が面積になります。台形を 対角線 の1本を境に分割すると2つの 三角形 になるがその三角形の 面積 比 は上底と下底の長さの比に等しい。 これは分割によって高さ(台形の場合は上底と下底の間の 距離 )の等しい三角形が2つできるためである。
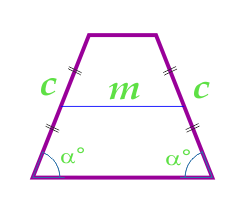



台形の面積




数学問題 知っている人は10秒以内に解ける台形の面積比の裏技 2問 Youtube
対角線BDが10cmの正方形ABCDがあるとしよう。 この正方形の面積の求め方は、 (対角線)×(対角線)÷2 = 10×10÷2 = 50cm^2 になるんだ。 どう?? 公式便利でしょ!?? なぜ対角線で正方形の面積を計算できる?? でもさ、 なんで「対角線だけ」で計算でき台形が対角線ACとBD(右図)によって4つの三角形に分割され、Oで交差する場合、 {\ displaystyle \ triangle} の領域148>AODは、 {\ displaystyle \ triangle} BOCの値と等しく、 {\ displaystyle \ triangle} AODの面積の積です。 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360
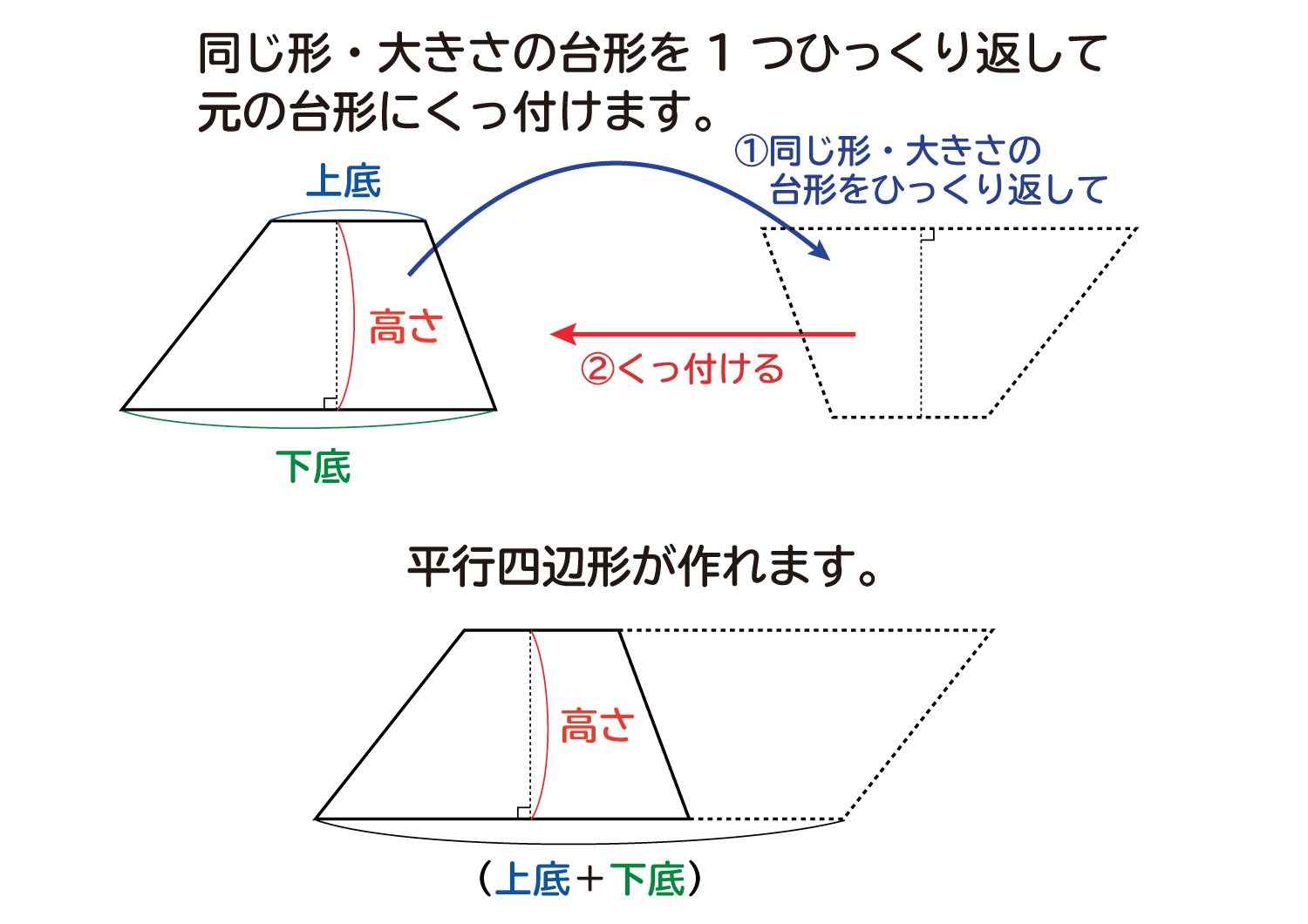



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
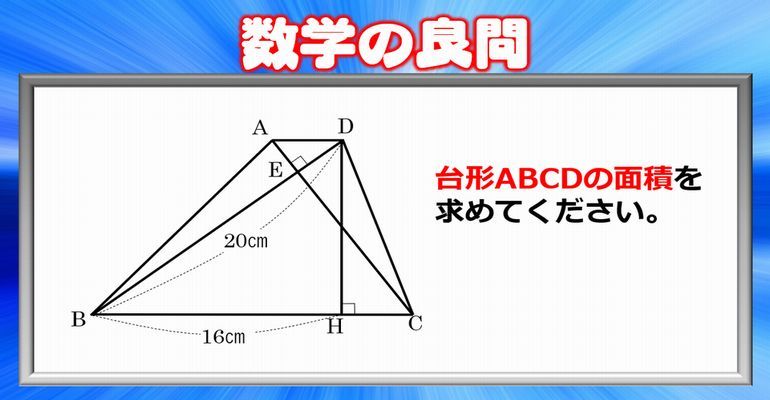



数学図形 解けたらスッキリする台形の良問 子供から大人まで動画で脳トレ 楽天ブログ
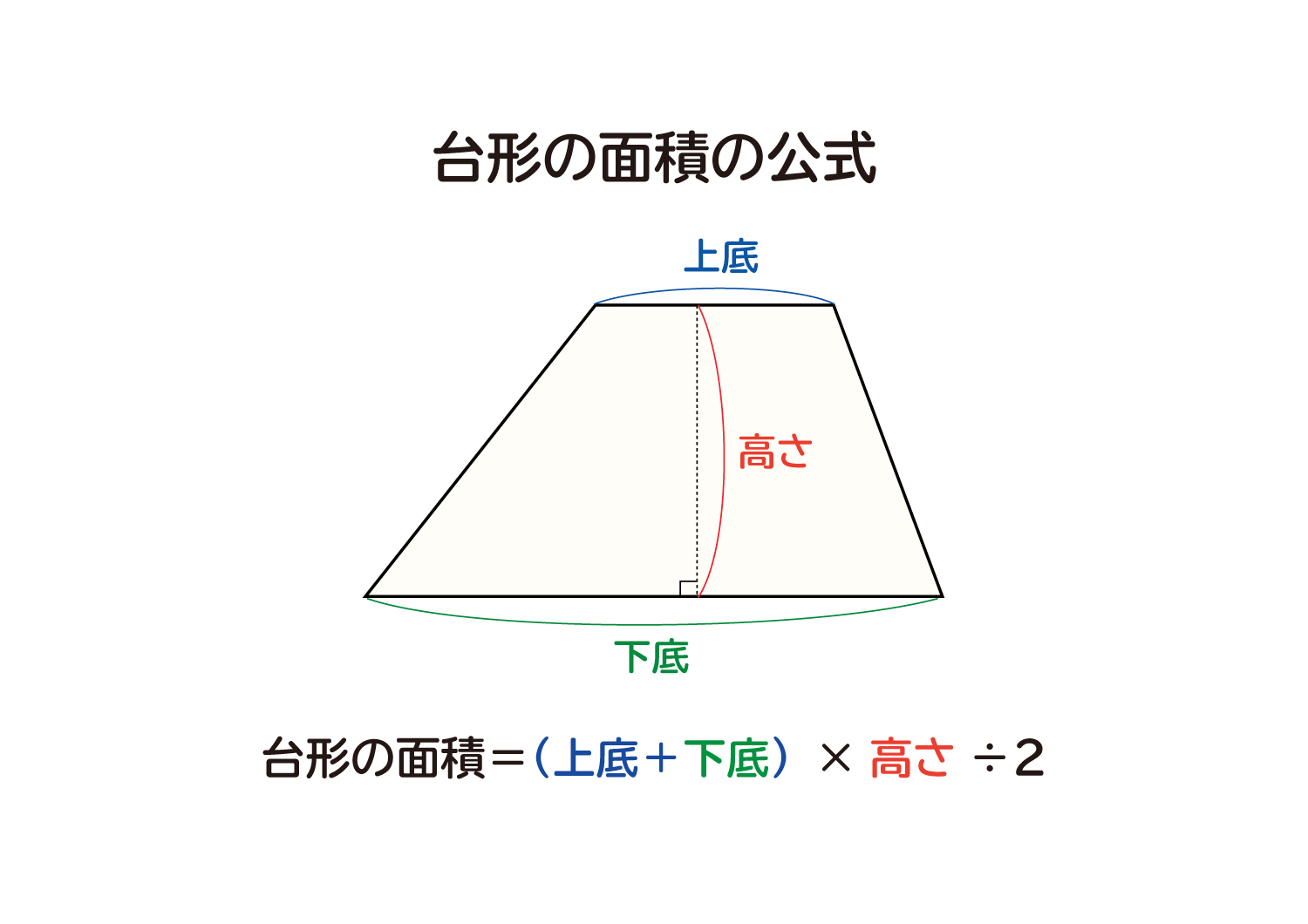
比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。 つまり、台形の中から相似な図形を見つけていくことがポイントになってくるね。 相似な図形において、面積比は相似比の2乗になる 比べる三角形が相似でなくても円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円 台形の面積の公式 台形の面積を 、高さを 、上底を 、下底を とすると、 (台形の面積) (上底 下底) (高さ)
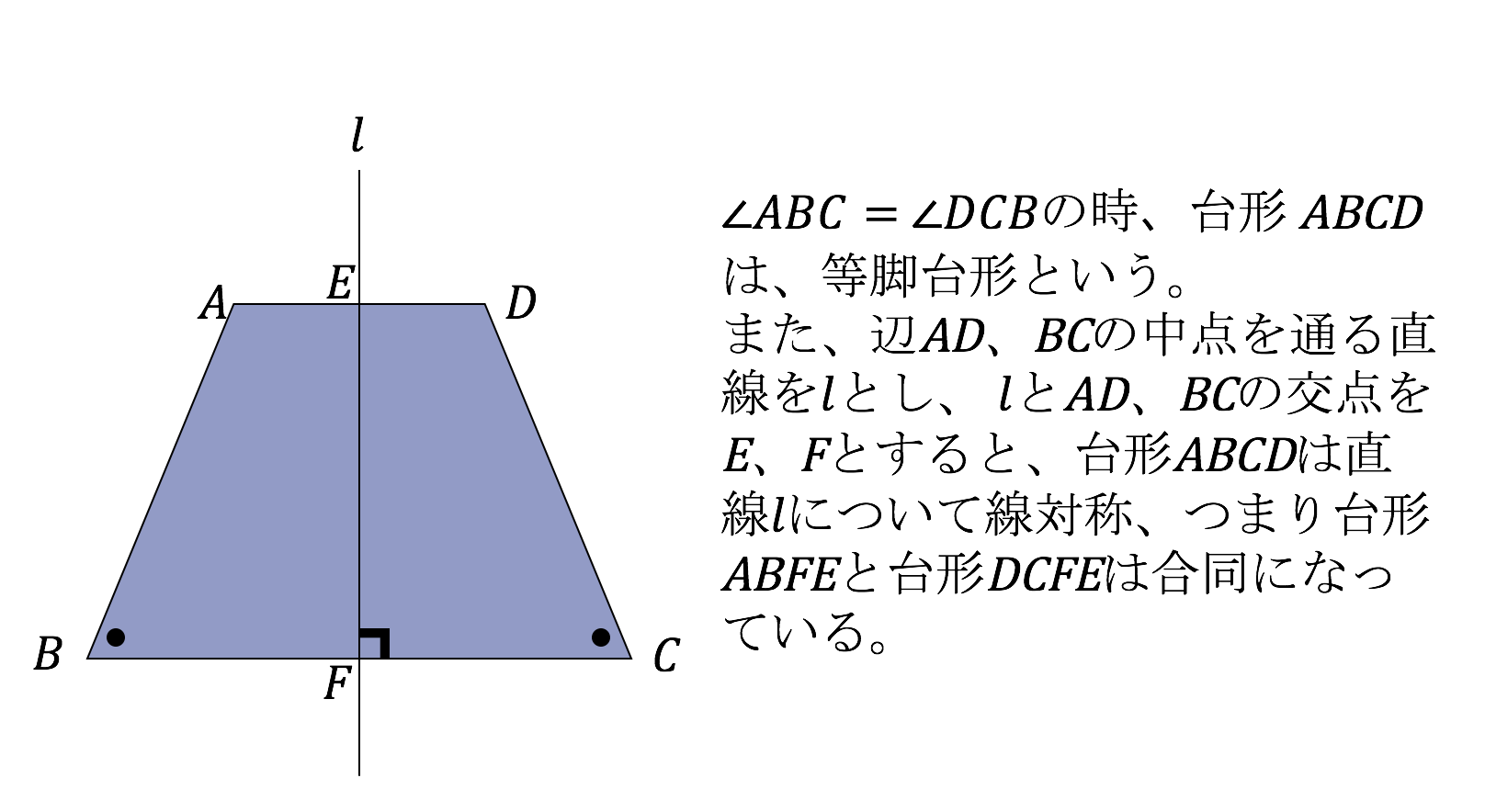



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ



中点連結定理




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



3
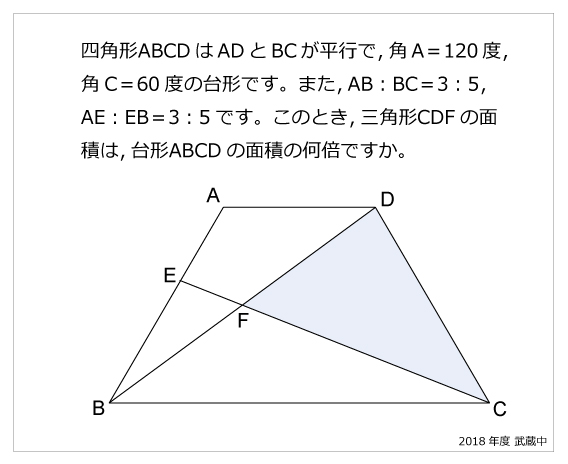



今年の1問 18年武蔵中 等脚台形 算数星人のweb問題集 中学受験算数の問題に挑戦
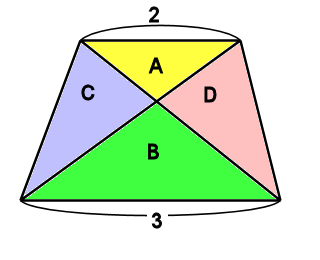



台形を切って




平面図形の苦手を解消 三角形の面積比 基本編
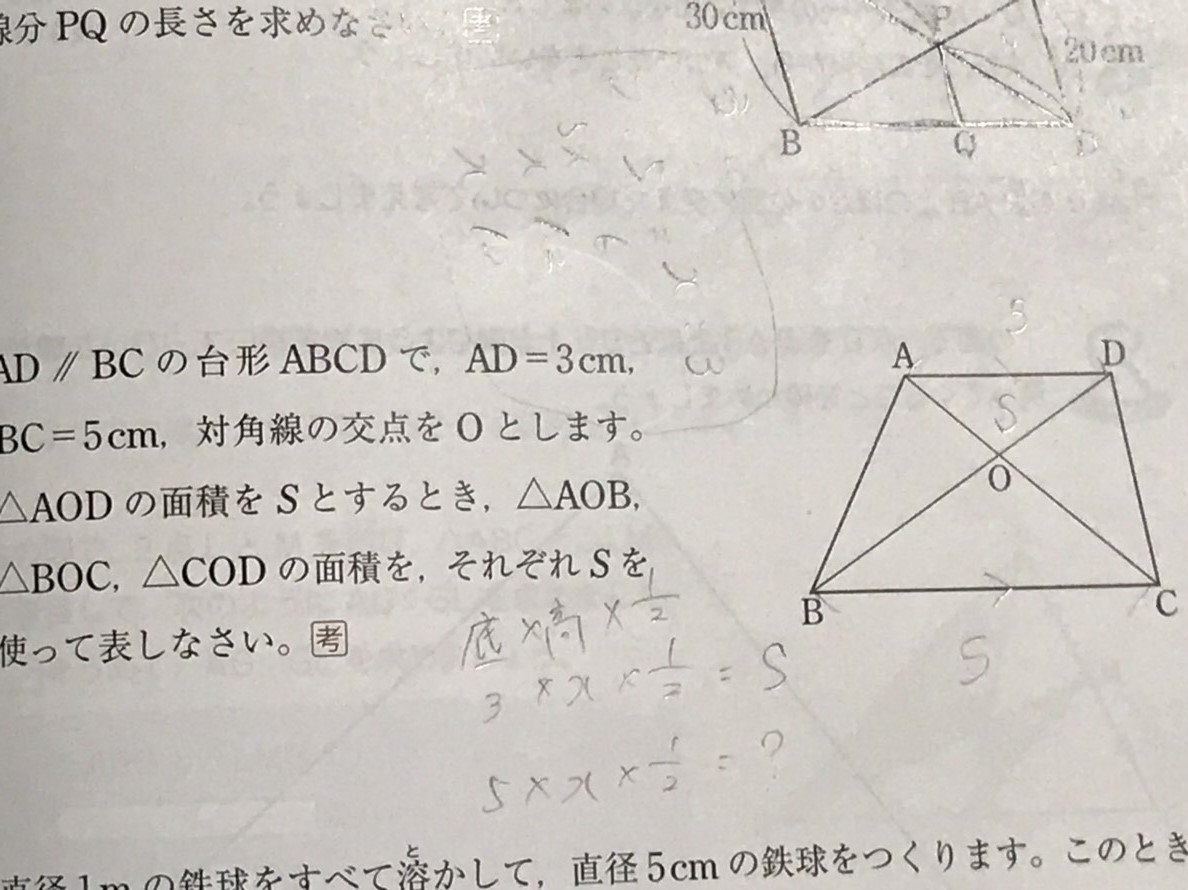



面積比
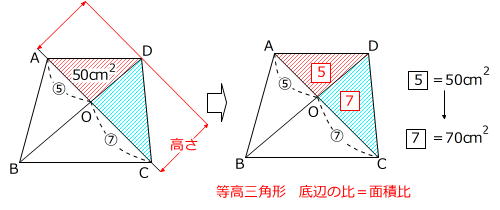



第415回 平面図形 の勉強方法 3 前田昌宏の中学受験が楽しくなる算数塾



補助線の引き方 日々の学習 兄中学受験




No 4 Adbc Abcd Ac e Lihat Cara Penyelesaian Di Qanda




台形の面積比 中学3年数学 Youtube



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



相似 台形と面積比の問題を徹底解説 数スタ
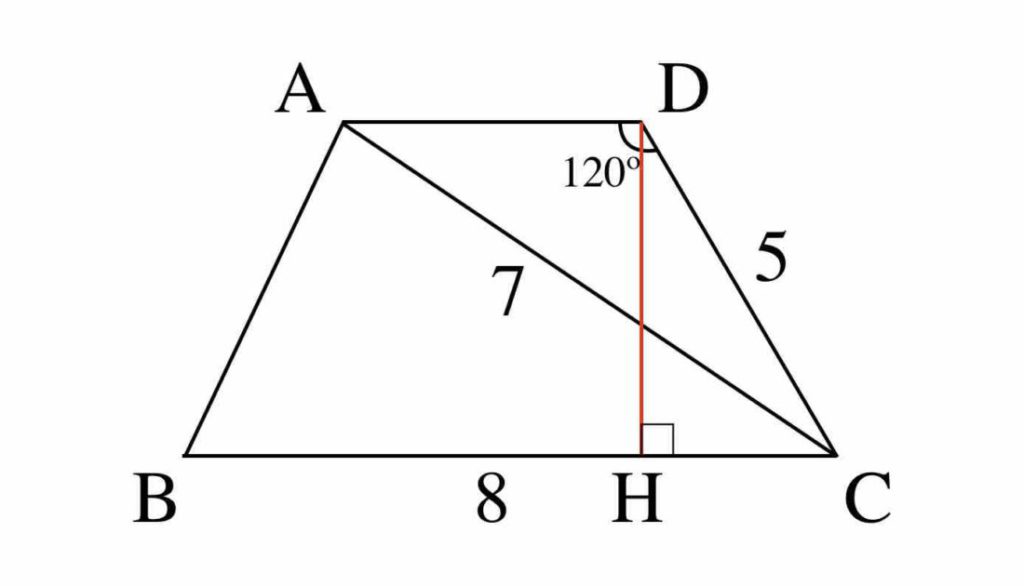



三角比を用いた面積計算をマスターしよう スタディクラブ情報局




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



入試問題に挑戦第84回




基本のquadrilaterals 四角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




問題2の 2 について質問です なぜ 相似な図形の面積の比であるのに Clear



5年算数面積2 教え方のポイント
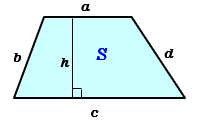



台形の1辺 面積 3辺の長さと高さから 高精度計算サイト



三角比を用いた面積計算をマスターしよう スタディクラブ情報局



Http Cms Nerima Tky Ed Jp Weblog Files 142 Doc Pdf
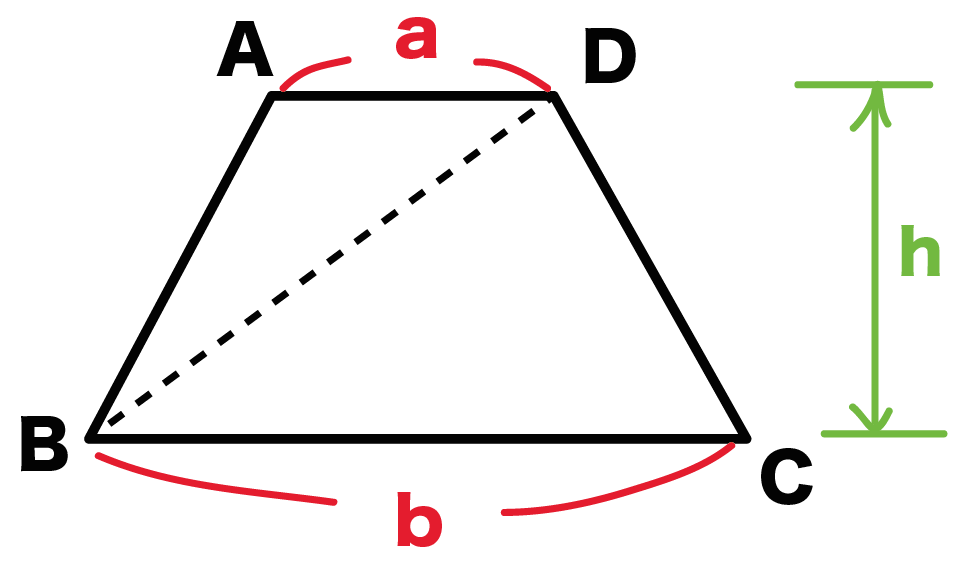



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
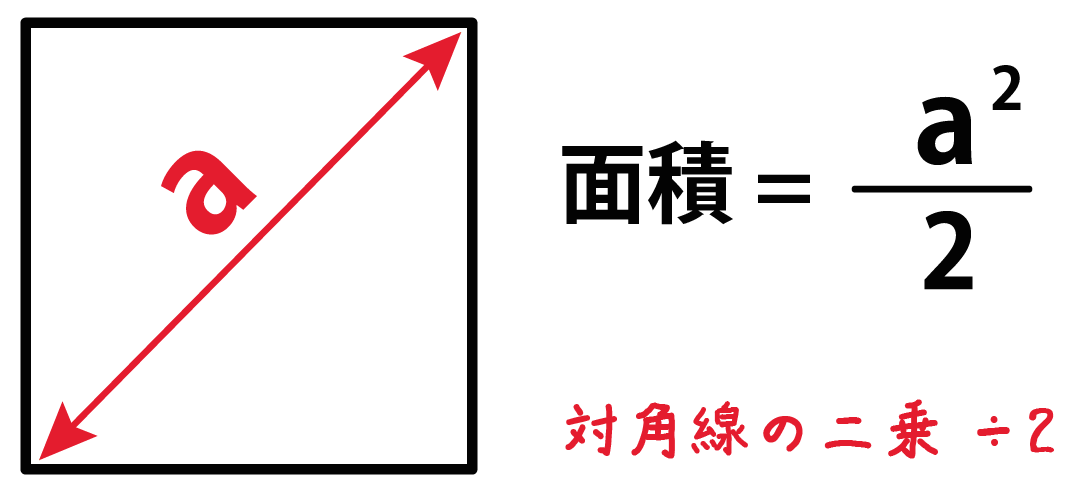



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
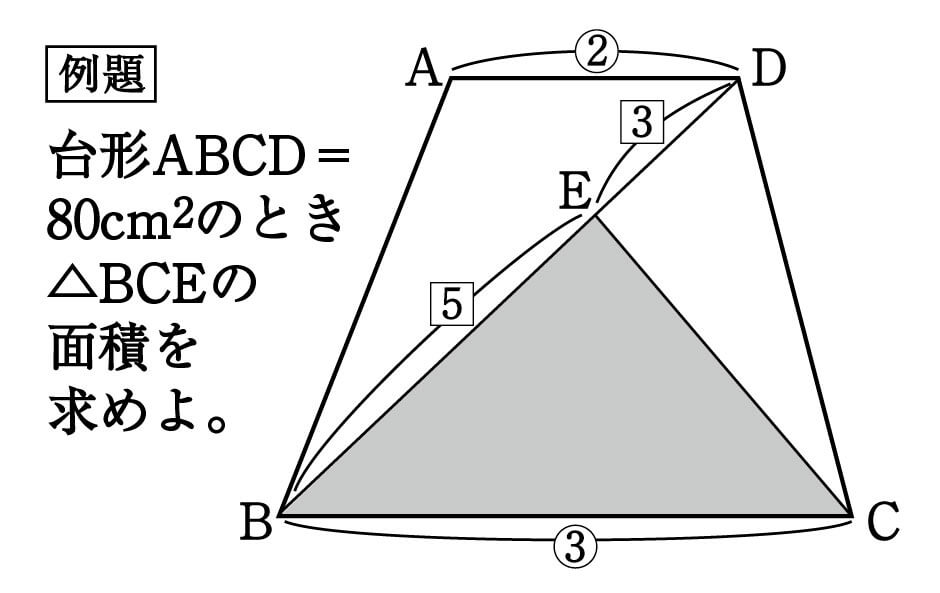



数学 対角線の入った台形 一角共有の三角形 面積比 集中特訓 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




等積変形とは 台形から三角形に変える問題を解説 応用問題 難問アリ 遊ぶ数学
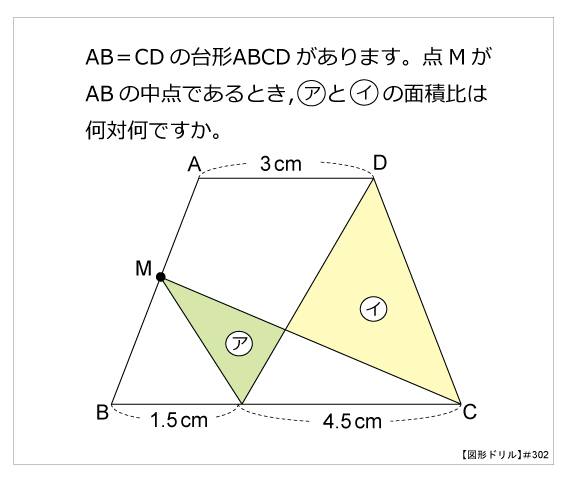



図形ドリル 第302問 等脚台形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




等脚台形において 2本の対角線の長さが等しいことの証明 うさぎめし C
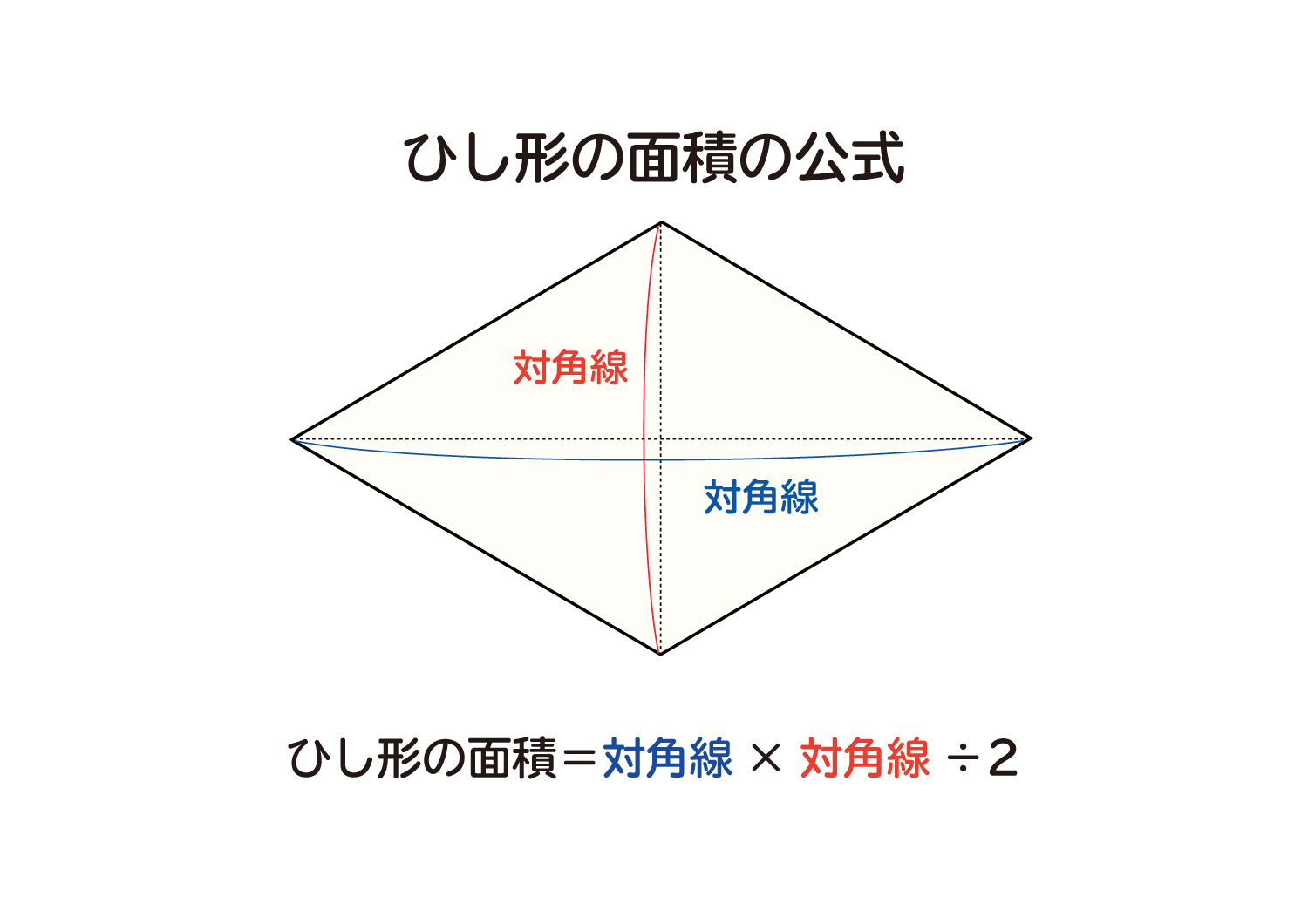



なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル




中3数学 相似 台形の対角線 Youtube
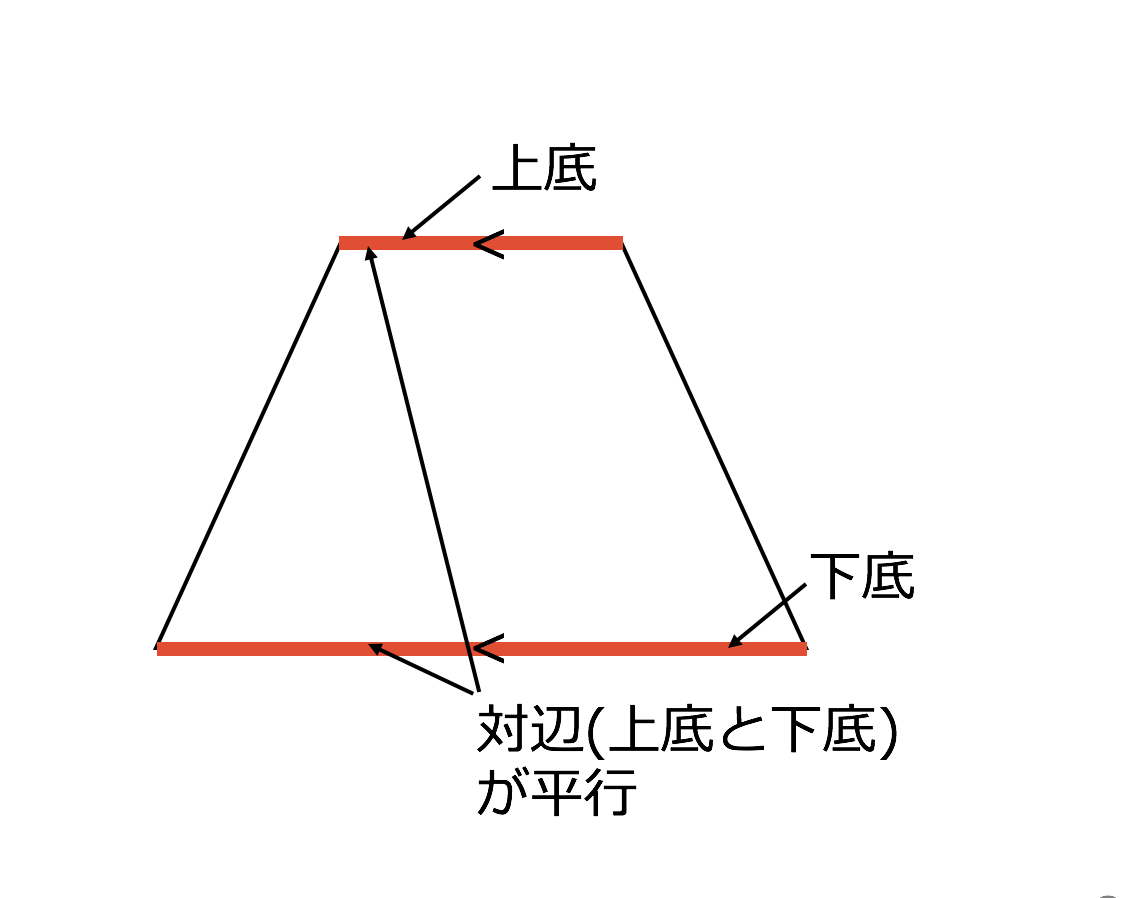



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ
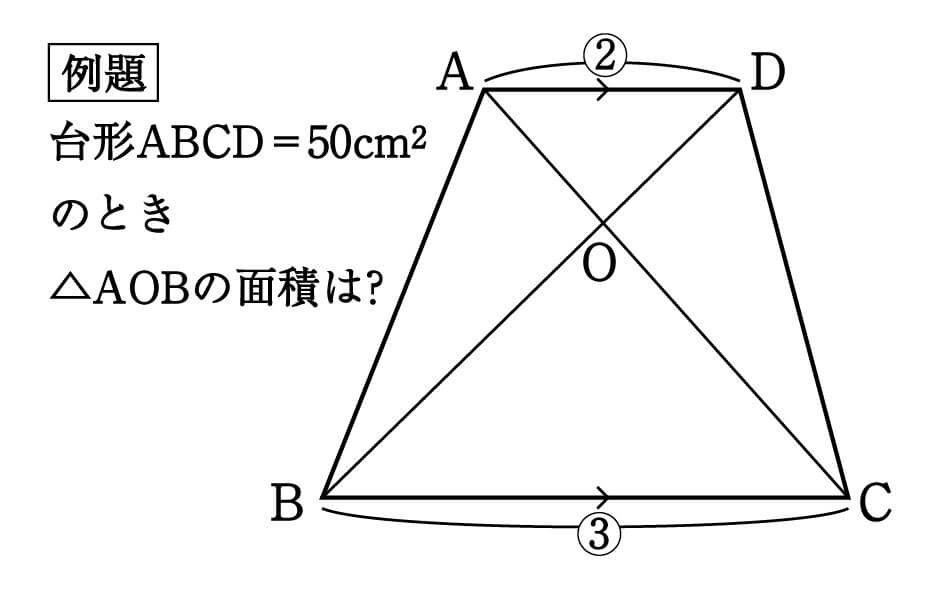



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



面積分割




小学5年生 ひし形 台形の面積 算数 Active Learning 学院




4 Adbc Ac Descubre Como Resolverlo En Qanda



Studydoctor台形の面積比 中学3年数学 Studydoctor
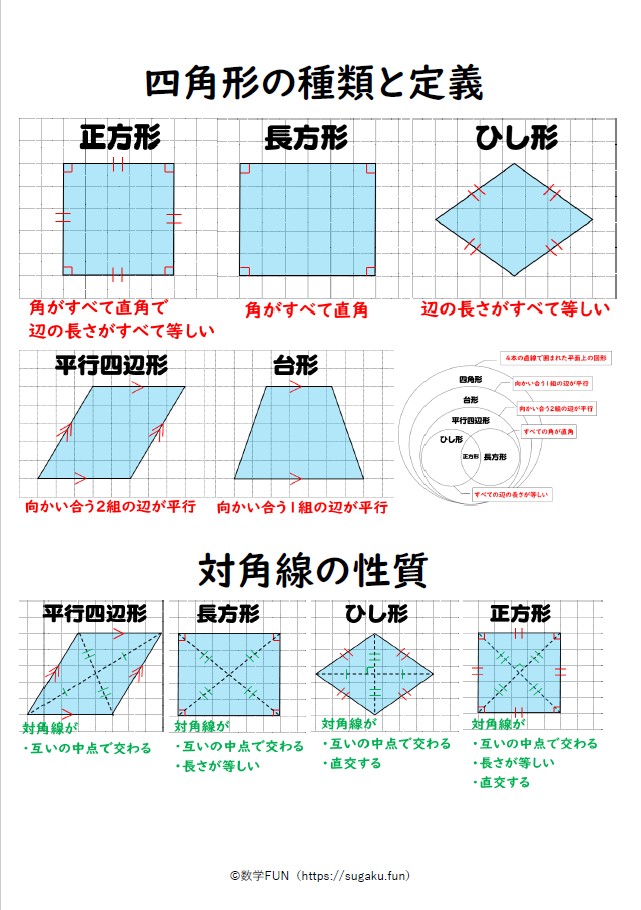



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




等脚台形 Wikipedia



5年算数面積2 教え方のポイント




小5算数 図形の面積 指導アイデア みんなの教育技術




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



面積分割
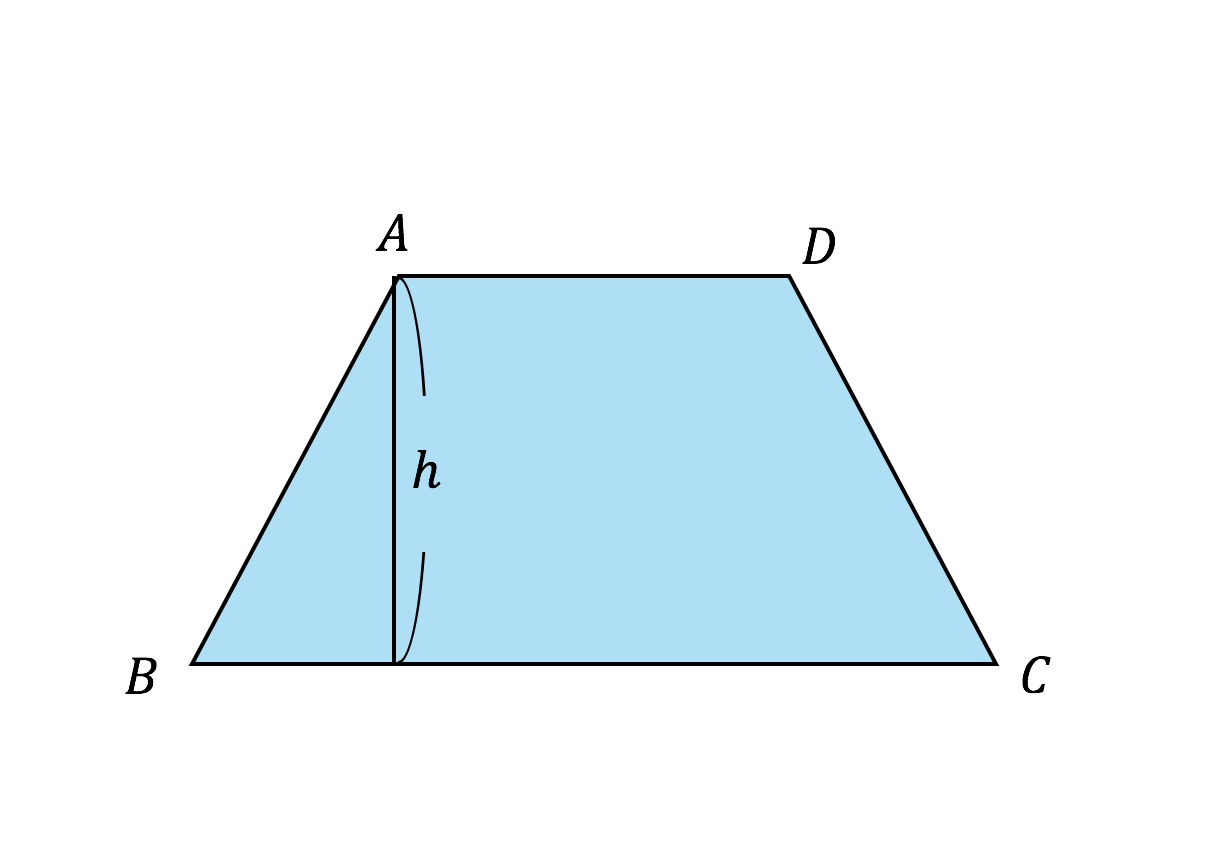



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
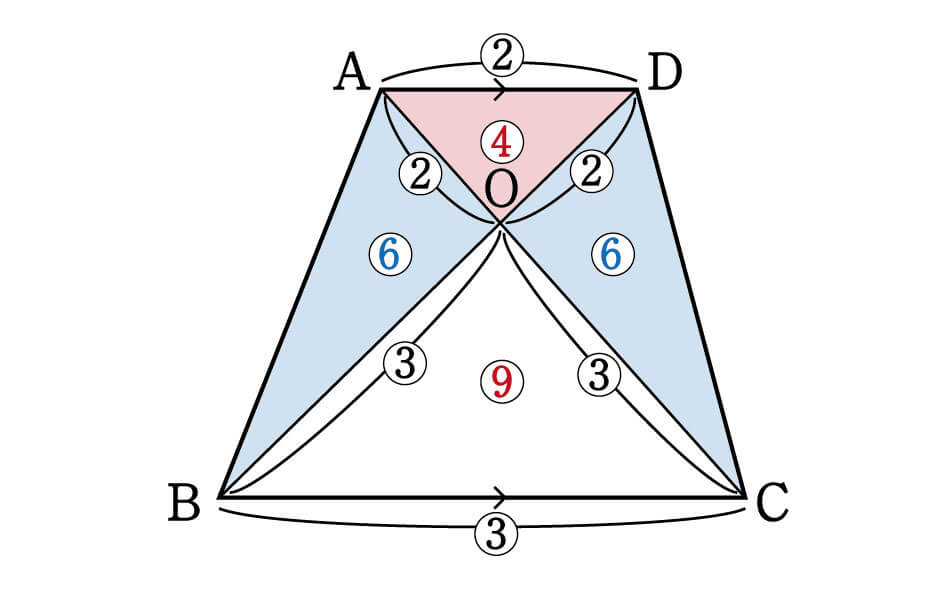



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



面積が等しい三角形 苦手な数学を簡単に




長女の中学受験 算数の復習で最低限覚えておきたい 図形の比の利用をいくつか確認しました Pi Sukeのネットな生活



3



台形の対角線をひいた時にできる三角形の面積比について なぜこのような Yahoo 知恵袋




解答編 補助線引けば秒殺 正六角形と台形の面積問題 小学生でも解ける問題です



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




中3の数学の問題が分かりません 下の写真の図の時 1 Pq Qr Rs Okwave




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題




台形の面積



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



同志社中学校2001年第8問 解答 解説
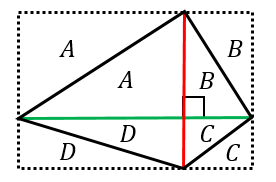



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




こちらの問題についてです Clear



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
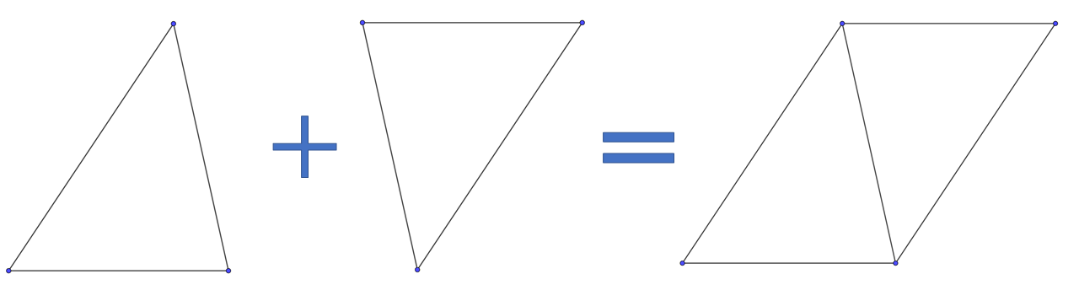



台形の面積が苦手 を克服する方法 中学受験ナビ




台形の面積 数学が嫌いなんです



算数の問題です 下の図の台形で 対角線で分けられる4つの部分の面積 Yahoo 知恵袋




平面図形の苦手を解消 三角形の面積比 基本編



台形の内側に対角線を2本引き 向かい合った左右の三角形の面積が同じだと言う事を Yahoo 知恵袋
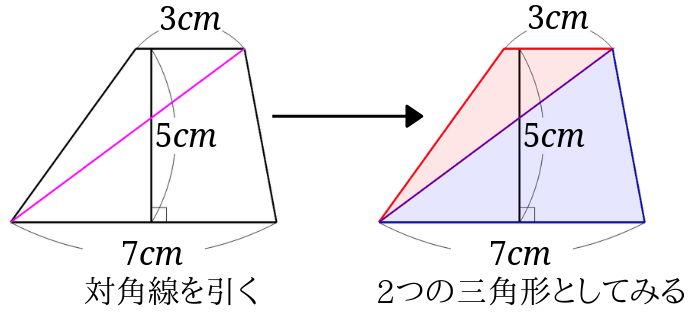



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




正方形の対角線で面積を求めることができる 知らない人も多いぞ 中学や高校の数学の計算問題




未だアクセスの多い 等脚台形 に関するブログ 中学校数学風に等脚台形の性質の整理をしておこう 身勝手な主張



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



5年 面積



Http Www Nikkei Com Edit News Special Gakute Shougaku Kaisetsu Sansuu4 Pdf



3




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch
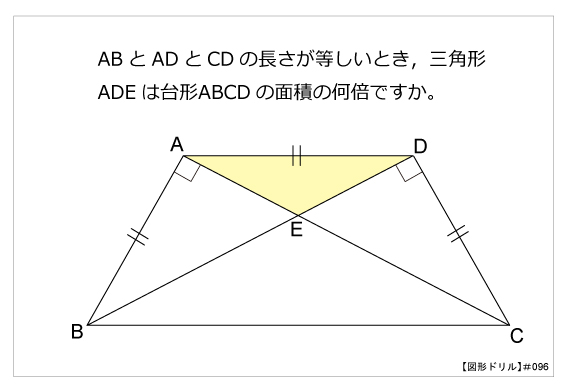



図形ドリル 第96問 等脚台形と三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
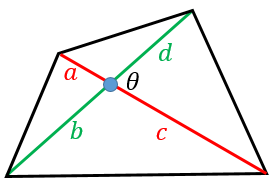



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




4 Adbc Ac Descubre Como Resolverlo En Qanda
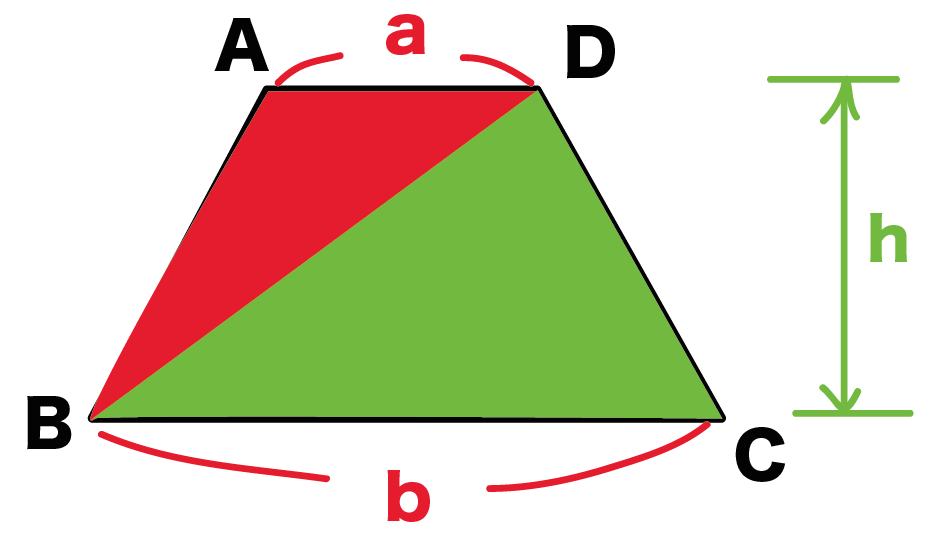



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




5年算数面積2 教え方のポイント
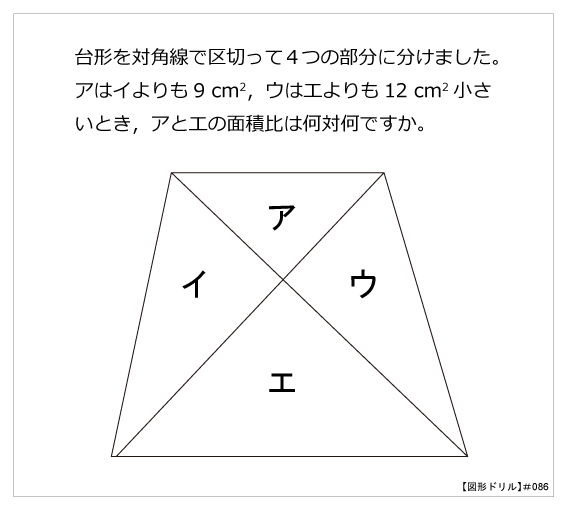



図形ドリル 第86問 台形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



Www City Sapporo Jp Kyoiku Shido Documents 2 2 3 27 Pdf
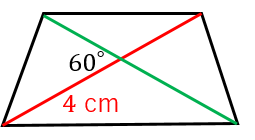



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学
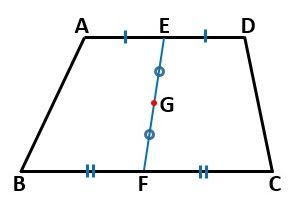



台形の面積の2等分線 東久留米 学習塾 塾長ブログ



1
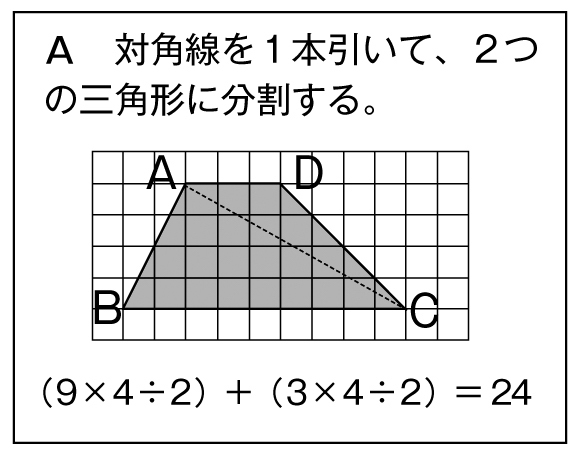



小5算数 図形の面積 指導アイデア みんなの教育技術




平面図形の苦手を解消 三角形の面積比 基本編
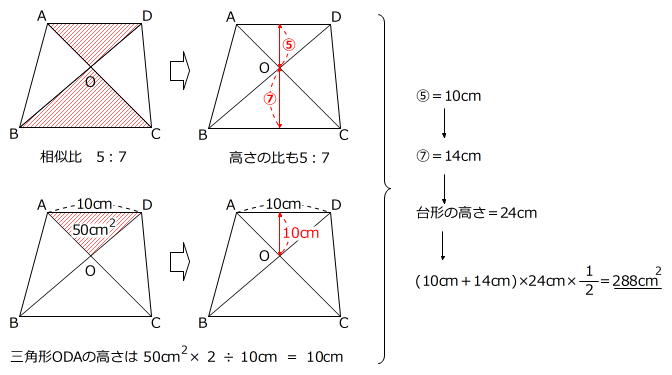



第415回 平面図形 の勉強方法 3 前田昌宏の中学受験が楽しくなる算数塾



4角面積



0 件のコメント:
コメントを投稿