三角形の定理はピタゴラス 歌 155331-三角形の定理はピタゴラス 歌

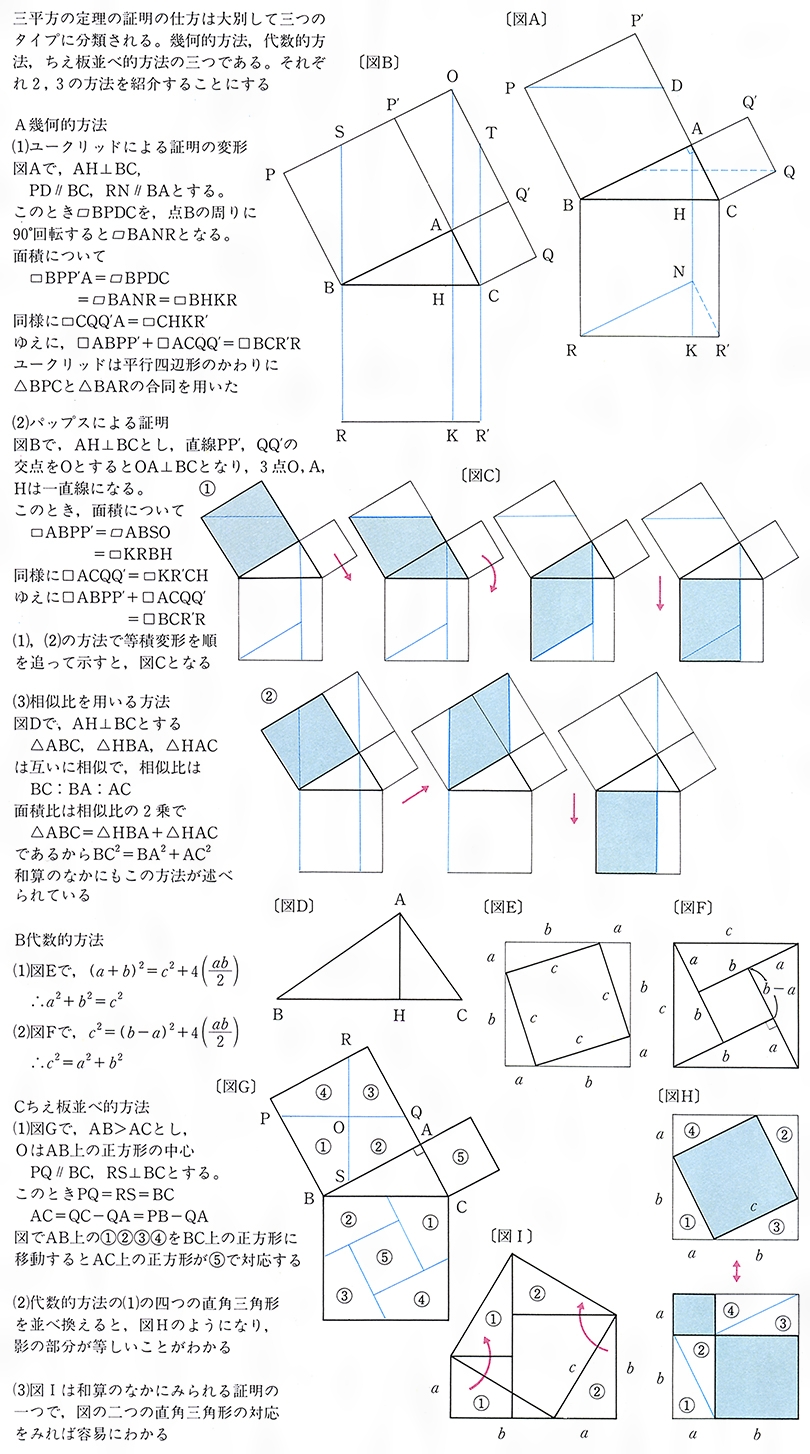
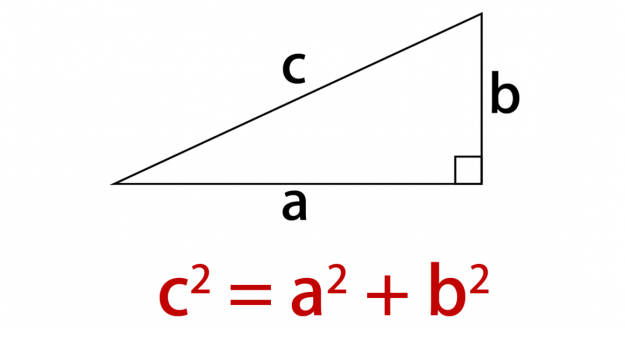
ピタゴラスの定理 図のような3つの辺の長さが，それぞれa, b, c である 三角形ABCにおいて， B A C a b c 角Cが90 の直角三角形⇐⇒ a2 b2 = c2 体験授業（数学） 7/ 78余弦定理の証明と例題 具体例で学ぶ数学 > 図形 > 余弦定理の証明と例題 最終更新日 余弦定理とは、三角形において が成立するという定理です。 目次 余弦定理の簡単な例題 6つの余弦定理 余弦定理の証明（鋭角の場合）ピタゴラスの定理 などしてくださる（／）。 直角三角形の斜辺の長さは、外接円の直径に等しく、また、直角をはさむ2辺の長さの和から、内接円の直径を引いた差に等しい。 中学数学の問題では3秒に一回ぐらい使う直角三角形の辺の比だから、 確実に覚えておこう。 18 な三角形を2つ並べ

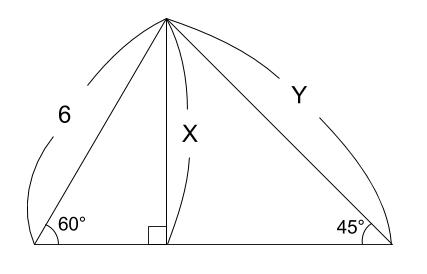
中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三角形の定理はピタゴラス 歌

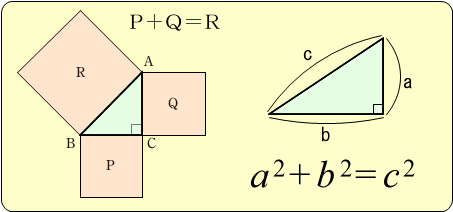
三角形の定理はピタゴラス 歌-ちなみにレ・ファ・ラを同時に叩くと暗い和音(短三和音)が響きますが、こちらは長三和音の時の直角三角形を裏返した直角三角形になります。 ↓ 図示するとこのような関係にある。 リンク Tweet List三平方の定理（ピタゴラスの定理） ∠ACB＝90°となる直角三角形ABCにおいて，各辺の長さを， BC= a BC = a ， CA = b CA = b ， AB =c AB = c とすると， a2b2 = c2 a 2 b 2 = c 2 の関係が成り立つ．この関係を 三平方の定理 あるいは ピタゴラスの定理 という．

ピタゴラスの定理byアインシュタイン Youtube

なぜ、そうなるのか？ 「ピタゴラスの定理」の証明方法は何百か、あるそうですが、今回は その中から1つ、相似を使った証明方法を紹介します。 まず、下図のように AB＝4、AC＝3、BC＝5 の直角三角形 ABCの点AからBCに直角に交わる線 (垂線)を書きます ピタゴラスより1000年早い ナゾロジー 土地区分のための「原始的な三角法」と判明 この粘土板は「Si427」と呼ばれており、実際に作られたのは、古代バビロニア時代（紀元前1900年〜1600年頃）です。 発見時には、描かれている図形が何を意味するのか直角な三角形でなくとも、「辺の長さの差」を求めたくなるのが人情です。 余弦定理と三平方の定理 ここで、余弦定理に戻ります。 a ^2 = b ^2 c ^2 − 2 bc cosA でした。 この形は意味を捉えにくいので、変形します。 b ^2 c ^2 − a ^2 = 2 bc cos A

ピタゴラスの定理は直角三角形に限定されているが、余弦定理は任意の角を持つ三角形で用いることができる。 ユークリッド原論では、⊿ABCで、γが鈍角となる三角形において、次が導かれるとする。 c 2 =a 2 b 2 −2ab cosγ なお、cos90°=0であるので、直角三角形の場合はピタゴラスの定理と完全じつは、三平方の定理（ピタゴラスの定理）のすごいところは、 直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる ピタゴラスの定理とは、直角三角形の底辺の2乗と高さの2乗の合計が、斜辺の2乗に等しいという定理です この定理は、建築設計で頻繁に使います また構造力学や構造直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは，1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理（ピタゴラスの定理)

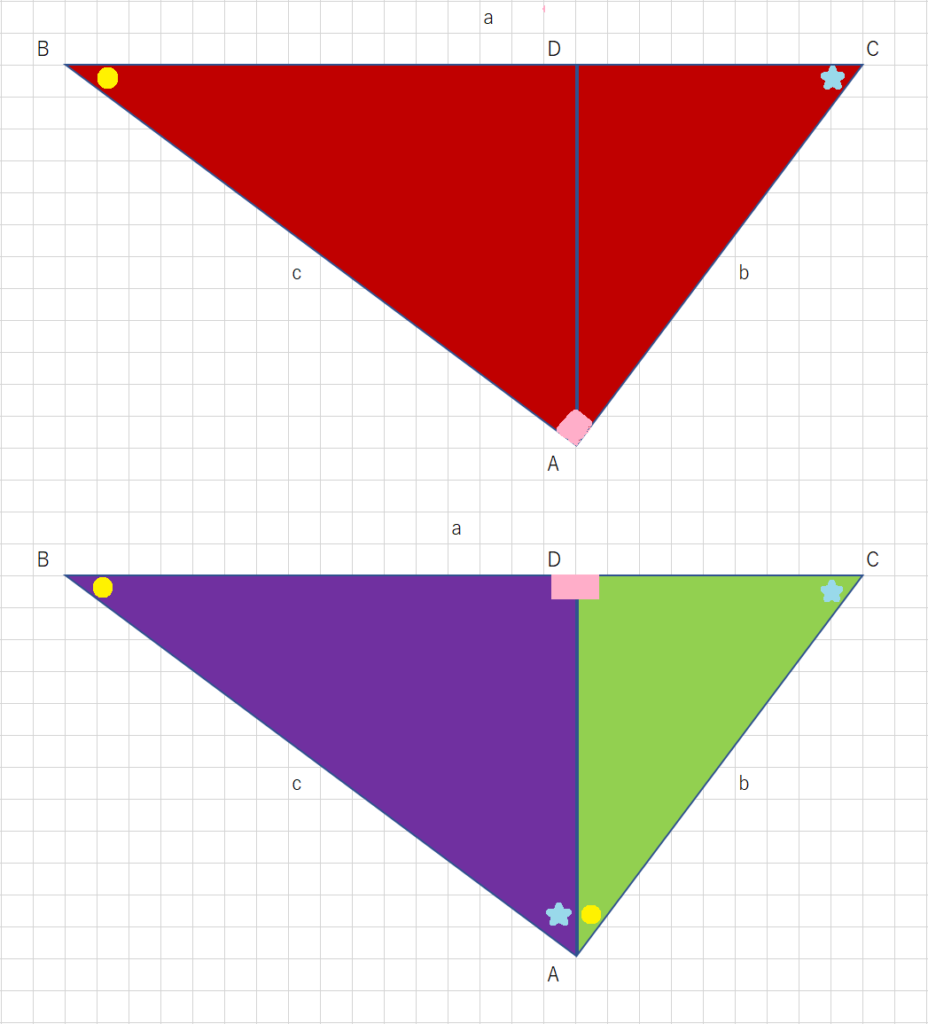
 では次に「ピタゴラスの定理」との関係を説明していきましょう。 まず「ピタゴラスの定理」とは、上にような直角三角形の一番長い辺（斜辺）を\(c\)、残りの辺の長さを\(a,b\)とすると、次のような等式が常に成り立つと、というものです。 \begin{align*} a^2b三角関数の公式は三角形の面積公式とピタゴラスの定理が分かっていれば簡単（受験の親指14） 数学は基礎から論理を積み上げる学問である。 数学は一つの論理的な帰結を多面的な視点から考察する。 小中高の学年ごとの学習過程を順番に学んでいくなお「ピタゴラスの定理」とは幾何学の有名な定理で、「直角三角形の斜辺の長さの二乗は、残る二辺の長さの二乗に和に等しい」、です。 図(1) 図(2) 少年アルバートは、直角三角形ABCで、辺の長さを図(1)のように、a、b、cとした。そして、C点から辺ABにおろした垂線CDによって、辺ABを長さ

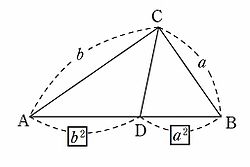
ピタゴラスの定理 Wikipedia

イアン スチュアート 世界を変えた17の方程式 ソフトバンククリエイティブ 有沢翔治の読書日記

 そんな数学的芸術のひとつの定理、 ピタゴラスの定理 を紹介します。 ピタゴラスの定理 ピタゴラスの定理は文字にすると、、、 直角三角形の「一番長い辺の2乗は、残り2辺の2乗の和」 になります。こちらを式にすると たったこれだけです。・逆ピタゴラスの定理 S．H 氏 直角三角形とくれば三平方の定理（ピタゴラスの定理）がすぐ思い浮かぶと思うが、最近 逆ピタゴラスの定理なるものがあることを知った。 逆ピタゴラスの定理 直角を挟む2辺の長さを a、b とし、直角の頂点から斜辺に下ろした垂線の長さを h とすユークリッドによる「ピタゴラスの定理（三平方の定理）」の証明です。Euclid's proof of The Pythagorean Theoremその他の動画#1レオナルド・ダ・ヴィン

中学生 歌う数学 三平方の定理のうた ニコニコ動画

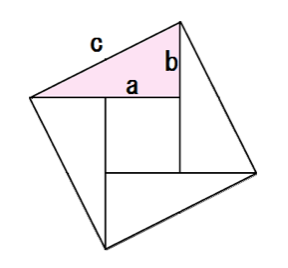
リンクの図に示すように 長方形の中に直角三角形が２つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora

（ちなみに、教団に入るためには、全財産を寄付し、俗世を断つ必要がある） その中で生まれた「ピタゴラスの定理」こと「三平方の定理」は 「直角三角形の斜辺の2乗は、他の2辺の2乗の和と等しい」 という直角三角形の3辺の関係を示したものだ。上の正弦定理・余弦定理が必要なので、始めにそれらを導こう。 授業では、余弦定理の証明のみを行います。正弦定理についてはテ キストの最後に参考として証明を載せてあります。 単位球（＝半径1の球）面上の三角形について次が成り立つ。 ピタゴラスの定理 ピタゴラスの定理の証明 この定理には数百通りもの異なる証明があり、例えば、「以下では頂点 a, b, c からなる三角形を abc と表す」「各辺 ab, bc, ca に向かい合う角を

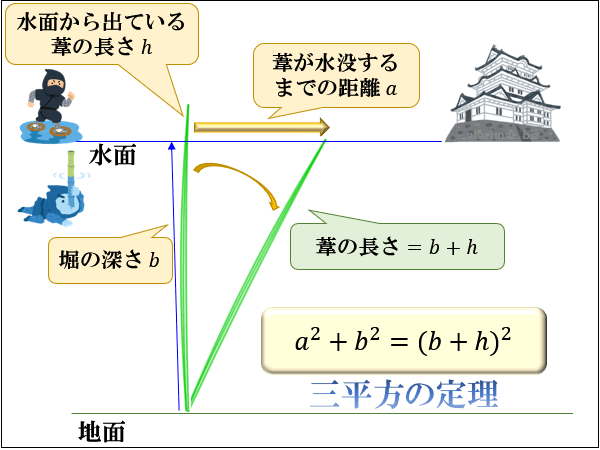
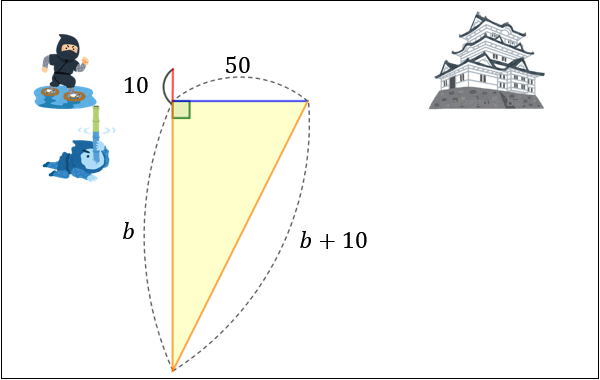
三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

ジャズと数学

はじめに 直角三角形の定理で、高校になってからもかなり活躍する定理をここで紹介します。その名も、三平方の定理（ピタゴラスの定理）です。 三平方の定理 まず図のような直角三角形ABCを描きます。 各頂点A、B、Cに対応する辺をそれぞれa、b、cと今回の「基本を考えよう」は前回に引き続き「ピタゴラスの定理」 です。 「ピタゴラスの定理」とは、直角三角形において、 のことでした。 なぜ、この公式になるのか、を前回示しましたが、証明の仕方は非 常に多いので、今回も、もう一つ有名な証明の仕方を示しましょう。 まず、三角形三平方の定理a b =c を成り立たせる3 つの 自然数a，b，c の組をピタゴラス数という。言うま でもなく，ピタゴラス数は直角三角形の3 辺の長さ を表している。たとえば， (a，b，c)=(3，4，5)，(5，12，13)，(8，15，17) な どは簡単なピタゴラス数であり，中学生にもなじみ 深いものであろう。 また

三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

人気の ピタゴラスの定理 動画 23本 ニコニコ動画

三角形PBTと三角形TCSが相似ですから、CS=2x(1x)で、ST=12x(1x)となります。 三角形TCSにピタゴラスの定理を適用すると、(12x(1x)) 2 =(1x) 2 (2x(1x)) 2 となります。正三角形の $1$ 辺の長さを②とすると、$1$ 辺はその半分なので①となります。残り $1$ 辺を三平方の定理を使って求めると、 三平方の定理 $1^2x^2=2^2$ これを解いて、$\textcolor{blue}{x=\sqrt{3}}$ よって、その辺の比は、$\textcolor{blue}{12\sqrt{3}}$ となります。 ② $\textcolor{blue}{45°,45°,90°}$ POINTそこで，ピタゴラスの三角形を利用してみよう． 底面の二等辺直角三角形を少しだけ変形し， A＝436度，B＝464度の直角三角形でよいことにすれば， 辺長を a：b：c＝：21：29 と整数比率にできる． これでは，二等辺三角形ではなくなってしまう． しかし，底面と側面とを正確に同じ寸法

中3 三平方の定理 例 ピタゴラス数 三角定規 Youtube

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

3，4，5 や 5，12，13 などです。この3つの数を3辺とする三角形は直角三角形で，古代エジプトでは縄張り師という人々が正確な直角を作るのに利用しました。ピラミッド建設にも利用したのでしょう。ところで，3，4，5のような連続したピタゴラス数は，他に ピタゴラスの定理を使って、良い比率の三角形を無限に生み出す 数学 Tweet Pocket ピタゴラスの定理（または三平方の定理）は、誰もが小学生や中学生の頃から知っている馴染み深い定理だろう。 ピタゴラスの定理を使って「3対4対5」など三辺のピタゴラスの定理は、直角三角形において、直角をなす2辺の長さを 斜辺の長さと関連付ける、幾何学の基礎的な公式です。 以下の図は直角三角形の斜辺の長さ（C）を直角をなす他の2辺（AおよびB）から 求める方法を示しています。 図： ピタゴラスの

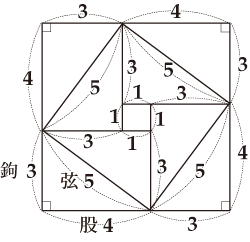
コラム ピタゴラスの定理 江戸の数学

ピタゴラスの定理の証明方法は何でしょうか Quora

相対性理論で有名なアインシュタインによる「ピタゴラスの定理（三平方の定理）」の証明です。PYTHAGOREAN THEOREM Proof by Albert Einstein#1レオナルド三平方の定理（ピタゴラスの定理）。 Cは直角三角形の斜辺になる。 様々な計算の基礎となる定理であり この式を利用すれば直角三角形であることが事前に分かっている図形の場合、各辺の長さを求める等が出来る 考えを発展させていくと 三角比と三角ピタゴラスの定理の一つの証明法（原 憲昭） rarc rr kanc >&13>' ― 2 ― ah が接角を2直角に等しくする。 それゆえΓa は ah と一直線をなす。 同じ理由で ba もaΘと一 直線をなす。そして角ΔbΓは角zba に，共に直 角であるがゆえに等しいから，双方に角 abΓが 加えられたとせよ。

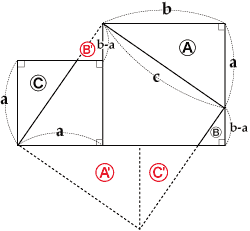
中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

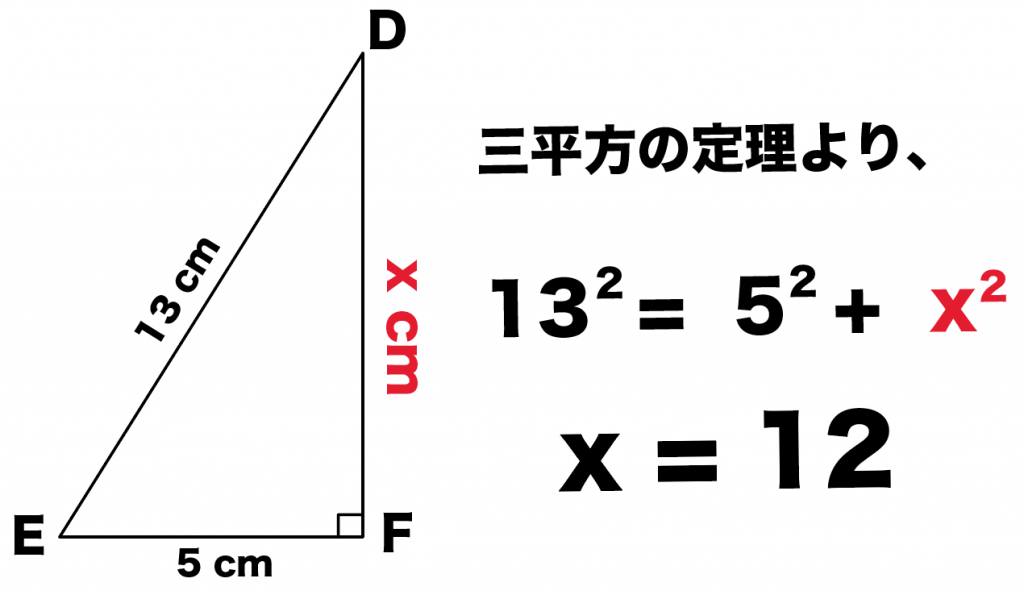
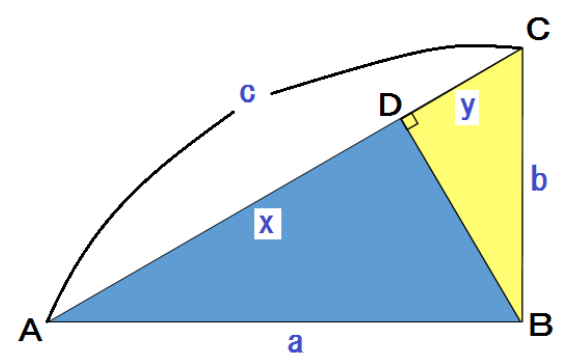
 三平方の定理（ピタゴラスの定理）を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理（ピタゴラスの定理）に代入してみると、 13² = 5² x² x = 12 あら不思議！ 長さがわからない直角三角形の辺を求めることができたね。 ＞＞ 三平方の定理双曲直角三角形の三角比 「k ピタゴラスの定理 以上の定理は，Bolyai が「空間論」で証明したものです．さらに，②,③,⑤より， ) sinh cosh sinh sinh cosh tanh cosA cosh = = = (cosine sinh cosh sinh cosh sinh tanh bcb bc b a cbcbc c = "⑥ 公式 ①，②，③より， sinB 1 1 sinh s si inh tanh tanA ·sinA (tangent ) cosA

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

位相のズレは90度

Mv チョッキー先生の三平方の定理 中3数学 Youtube

メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム

数学も英語も強くなる 意外な数学英語 Unexpected Math English December 15

バミューダ3 Twitter Search Twitter

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

雑学のソムリエ ヒポクラテスの三日月

三平方の定理 覚えておきたい基本公式を解説 数スタ

ピタゴラスの定理byアインシュタイン Youtube

Excel Vba 数学実験室 ピタゴラスの定理と円の方程式

三平方の定理について 三平方の定理は三角形の１つの が 必ず ９０ 数学 教えて Goo

名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理による古今伝授

こちらの問題は三角比で解けないのでしょうか 先生に聞いたとこ Yahoo 知恵袋

コラム ピタゴラスの定理 江戸の数学

三平方の定理とは コトバンク

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

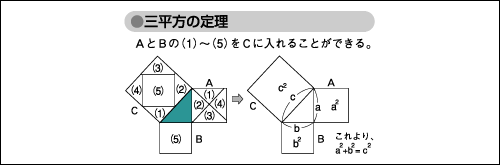
ピタゴラスの定理 時事用語事典 情報 知識 オピニオン Imidas イミダス

ピタゴラスの定理の証明方法は何でしょうか Quora

家に居ながらお小遣いを稼ぐ方法 直角三角形の 三平方の定理 のことを 別名 誰 の定理 という 脳トレクイズ

ウケる数学 地平線までの距離 自由気ままな放課後

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

多胡碑と縁がある様々な謎

書評 ピタゴラスの定理

数学の図形問題を日常生活にいかす デイリーポータルz

数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

三平方の定理 覚えておきたい基本公式を解説 数スタ

中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

直角三角形なら三平方の定理が成り立つ 逆は成り立ちますか また それを証 Yahoo 知恵袋

三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう

わにぱくら Wanichan W Twitter

大伴家持と三平方の定理

バミューダ3 Twitter Search Twitter

ピタゴラスの定理 難関大学 数学の発想のしかた さくら教育研究所 Skredu

見えますか タイルの模様からピタゴラスの定理 Note Board

三平方の定理 の新着タグ記事一覧 Note つくる つながる とどける

ピタゴラスの定理を使って 良い比率の三角形を無限に生み出す おとなぱすた

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

ますたこ クロ美 あの アキ子 これは一体 迅雷 トゥララ トゥララ トライアングル 三平方の定理はピタゴラス 今日12 5は バミューダトライアングルの日 だからな みんなでバミューダ3の名曲 恋の三角海域sos を歌おうじゃないか

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

ピタゴラスの定理 難関大学 数学の発想のしかた さくら教育研究所 Skredu

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

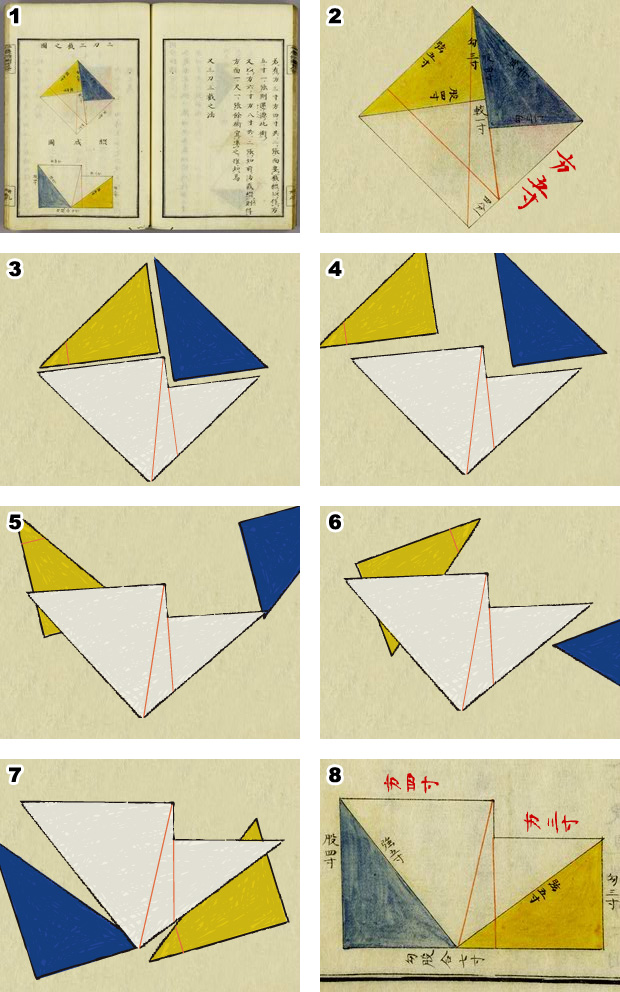
コラム ピタゴラスの定理 江戸の数学

メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム

リンクの図に示すように 長方形の中に直角三角形が２つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora

三平方の定理 の新着タグ記事一覧 Note つくる つながる とどける

中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

三平方の定理を英語で読んでみる

三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう

ピタゴラスの定理 Wikipedia

三平方の定理 覚えておきたい基本公式を解説 数スタ

ピタゴラスの定理 Wikipedia

ピタゴラスの定理 Wikipedia

コラム ピタゴラスの定理 江戸の数学

大伴家持と三平方の定理

三平方の定理 がひと目で分かる展示が面白いと話題に 視覚的にわかる こういうのが学校にあったら ねとらぼ

ピタゴラスの定理 難関大学 数学の発想のしかた さくら教育研究所 Skredu

人気の 三平方の定理 動画 33本 ニコニコ動画

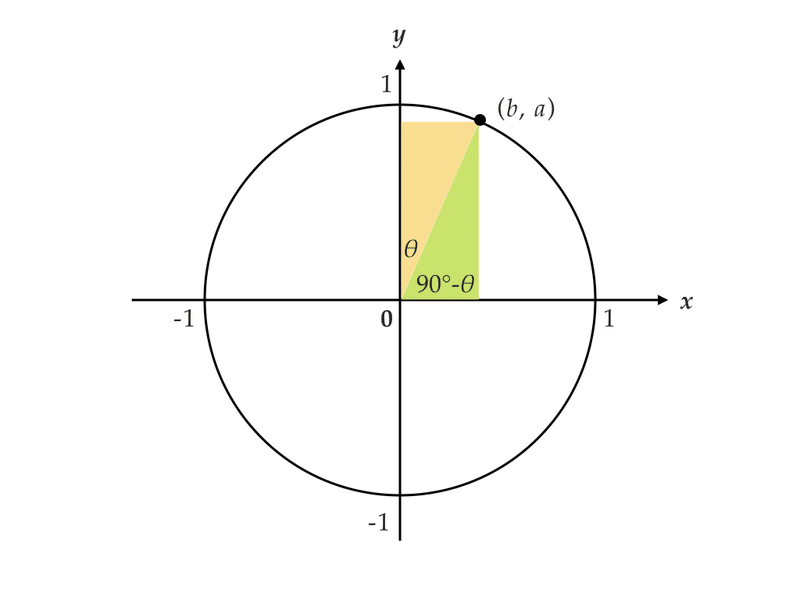
三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

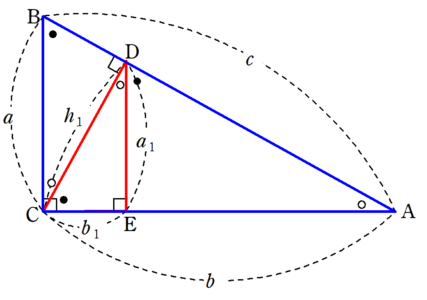
三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも

ピタゴラスの定理 視覚的に見て分かる三平方の定理の証明が面白い 物理エンジン Youtube

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

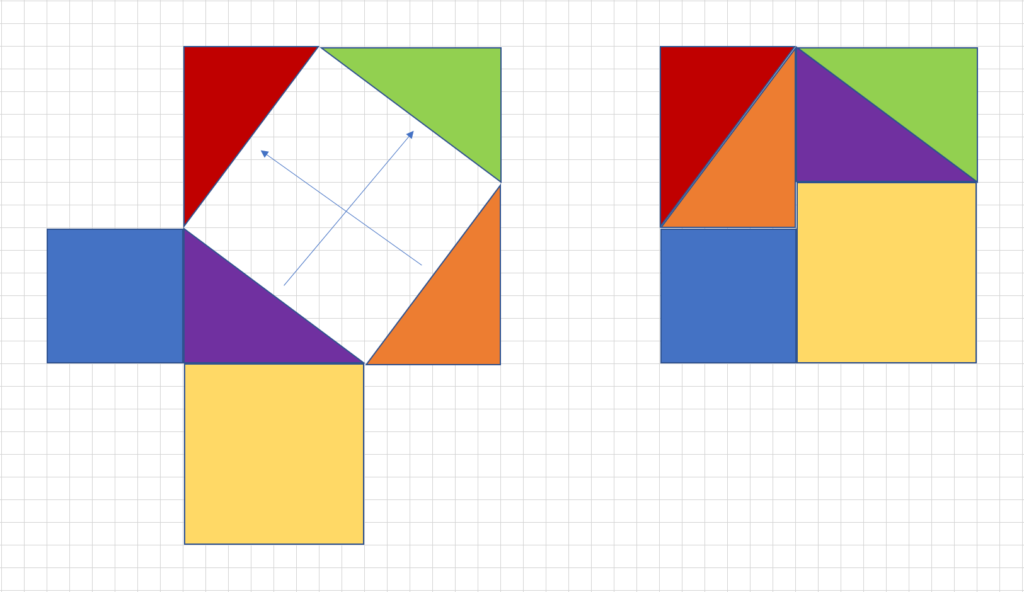
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

アルケー 万物の根源は 哲学者たちはどう考えた 知的な小話１８０ 読むと賢くなるブログ

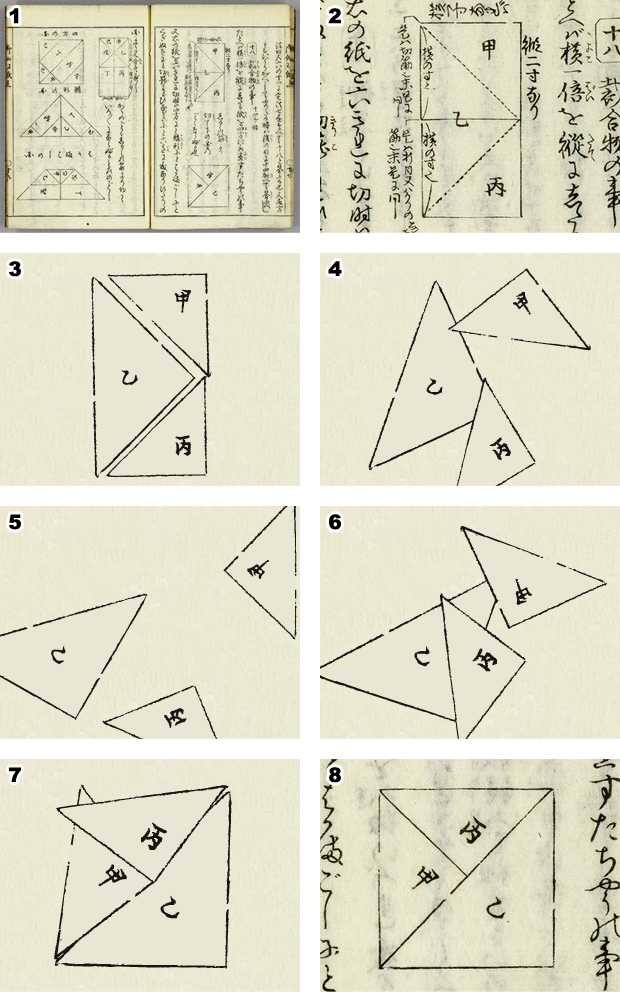
コラム ピタゴラスの定理 江戸の数学

恋の三角海域sosを1 25倍速にした方がしっくりくる説 Youtube

最新 ブログ 数学月間の会sgk

ピタゴラスの定理 の証明アニメ6 ユークリッド Youtube

三平方の定理に関係する暗号

リンクの図に示すように 長方形の中に直角三角形が２つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora

人気の ピタゴラスの定理 動画 23本 ニコニコ動画

人気の 三平方の定理 動画 33本 ニコニコ動画

Sirenというゲームで流れる 三平方の定理はピタゴラス という曲がありますが Yahoo 知恵袋

ジャズと数学

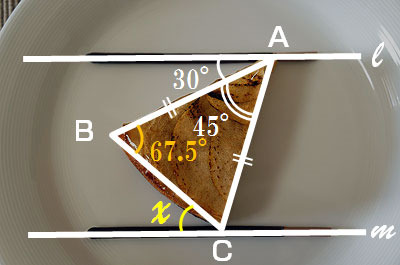
直撃 中学入試問題 第317回 広尾学園 平面図形 三角形 四角形の面積 北辰塾 情報局

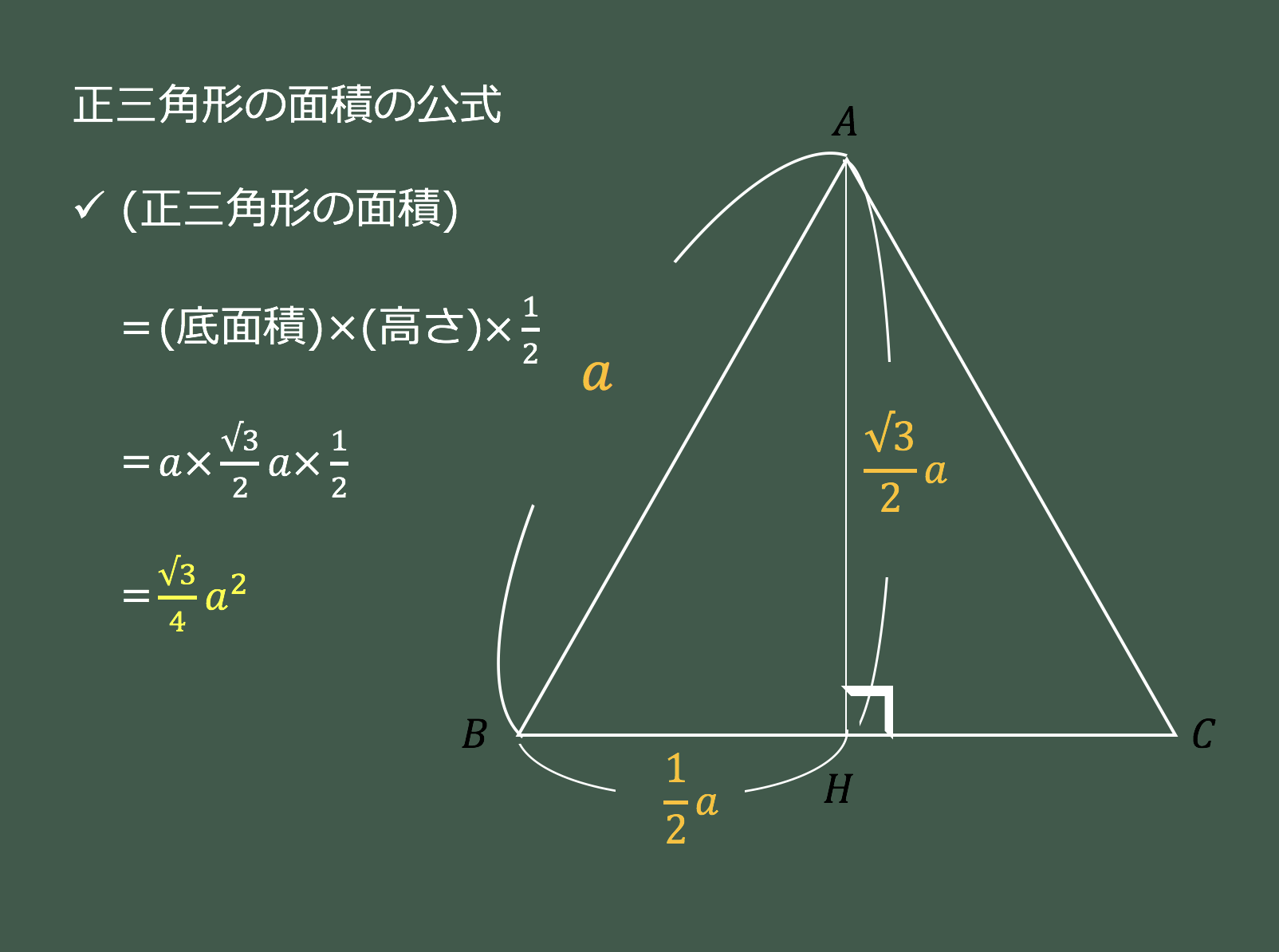
最高 50 正三角形 面積 求め方

三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう

Q Tbn And9gcroomicrnj3if9fk9rytc3of6r5axeu 8rxf94tbkv X Rmhoc Usqp Cau

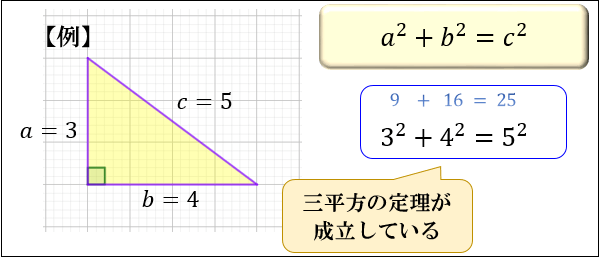
三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

Math 02 三平方 ピタゴラス の定理 Adobe Flash Cs3 Professional Actionscript 3 0

Incoming Term: 三角形の定理はピタゴラス 歌,